Eclipse:

Alison, you wrote :
"When we left, the ride took 10 hours instead of the 5 it took to arrive. Much of the first hours were spent inching with traffic leaving the nearby downtown, which we had to traverse to get back to the highway."

Wow! Thank you very much for relating this story. Delays post-eclipse are certainly a major concern. And, yes, we do have a plan to avoid this issue as much as possible. There are two miscalculations that I find that people make when planning total eclipse expeditions.

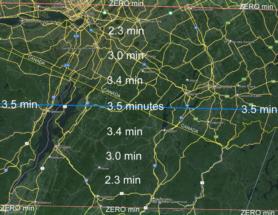
One issue: they try very hard to get on the exact centerline of totality. They push this. They sell this. And why not? It's a good way to make money! But it's completely un-necessary. As an example, I'm attaching here a map I made today for southern New England locals who are contemplating trips to northern Vermont on Monday. Notice the very broad zone around the centerline where the duration of the eclpse is essentially unchanged. Except for the fringes of the totality path, the view is good. Any locations within about 75% of the centerline are all about the same. Anyone who enjoys calculation, you can get the percentage of totality time easily. See the PS below.

Another mistake: they aim for "nice places". There's a certain charm in this, of course, but it can lead to practicality headaches. Instead we aim for simple, boring places, like large, empty parking lots less than one mile from an interstate highway access point. We have an extensive list!

Frank Reed
Clockwork Mapping / ReedNavigation.com
Conanicut Island USA

PS: Don't like math? Then don't read this! ;) To calculate the fraction of totality to expect at points inside the path of totality but off the centerline, look at your point of observation on a map of the path. Its distance from the centerline to the path edge can be counted as some fraction, ƒ. You can estimate this visually. Then if the centerline duration of totality is some time, T₀, your actual time of totality, T, will be T = T₀ × √1 - ƒ². It's just the equation for a circle (or a projected ellipse) since that is the shape of the Moon's "umbra". Example: suppose centerline totality is four minutes (as it will be in and near Shelbyville, Indiana). Suppose you're 25% off the centerline. Calculate it, and you'll find that the eclipse duration is shorter by less than eight seconds —insignificant, just 3%, out of 240 seconds. Note that this calculation is an approximation but it is a high-quality approximation in most practical cases.

File: