NavList:

   

Reply

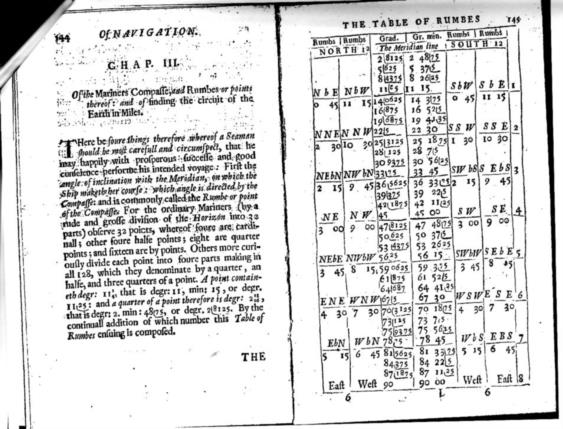
Paul Hirose pointed us to a Google of Briggs book on Logarithms, of 1624.

The Latin text, in that, defeats me, but I was interested in Briggs'
notation for decimal parts of numbers, which were quite a new concept in
those days. Until then, the Western world had relied on fractions.

The "decimal-point" (or in Europe, "decimal-comma") hadn't yet come into
use, and mathematicians denoted decimal numbers in whichever way they
thought best.

Briggs denoted the integer part of a decimal number by slightly larger type;
then the decimal part, in smaller type, was underlined. In the attachment
you can see how the printer has set it out, by inseting a row of underline
characters, rather raggedly, into his block.

My interest comes from reading an account by Oughtred of his circular slide
rule, of about 1630, which he called his "Circles of proportion", comprising
11 concentric scales, finely inscribed on a brass disc 18 inches diameter.
The book has an addendum concering his navigator's version, which is the
instrument held at the Museum fot the History of Science in Oxford. That
version has a two-turn scale of meridional parts, two turns (decades) of log
sines (of angle from half-a-degree to 90), and four decades of log tans,
from half-a-degree to 89.4. It was intended for handling the navigational
problems of rhumb-line sailing, but not (as far as I can make out) to handle
the great-circle calculations that the Bygrave is designed for.
Nevertheless, I imagine that with a bit of fiddling, by taking complements
of angles, a similar 3-step process to that used by the Bygrave might be
implemented.

But all that is by-the-way. What I wanted to ask about concerns a
translation from his original Latin of Oughtred's 1632 book about his
Circles of Proportion. It's the second, corrected, translation, this one by
Arthur Haughton, of 1660. It's been digitised, by EEBO (Early English books
online) but only available to subscribers, such as university libraries.

And my question has little to do with navigation itself, but with Oughtred's
notation for decimals, which is, I think, the same notation that was being
used in the earlier documents of 30 years before, just a few years after
Briggs.

Oughtred goes to some trouble to explain about decimals, and his notation
involves drawing an L-slaped line, the vertical stroke coming beteen the
units and tenths digits, when it bends to the right to underline all of the
decimal-part. You can see many instances in the attachment, oughtred.jpg.
What I found so interesting was that all these L-shapes differ, noticeably.
Of course, you expect the horizontal stroke to be of different length, for
differing numbers of decimal digits, but it's more than that. Sometimes, the
bend of the L is sharp, in others, it's rounded. Sometimes, the "horizontal"
arm is casually sloping, by different amounts.

I wondered how these marks had been put into my copy, and indeed, whether
they had been laboriously drawn in, in manuscript, after printing. By a
stroke of luck, the museum happened to have a second copy of that same
edition. [It's hard enough to lay hands on a 17th century book, never mind
finding two identical copies in the same place] And indeed, those L marks,
in the two copies, were identical; they had indeed been printed.

So now, at long last, I get to my question. HOW were they printed? The
museum librarian hazarded a guess that the printer had somehow inserted bits
of bent wire into his block, to pick up the ink and transfer it. But how
would they be held in place? Does anyone know enough about printing to make
a guess?

Life, for printers of such technical matters, must have got a lot easier
once the decimal point came in.

The attachment itself is interesting to navigators, in its content. It shows
the four quadrants of the compass, each divided into 32 "rumbes", but those
angles are precisely split up, and given  in two alternative decimal
notations. Either as decimal degrees, starting at 2.8125 degrees, or as
degrees and decimal-minutes, starting at 2 degrees 48.75 minutes. Oughtred
was a long way ahead of his time, in decimalisation.

George.

contact George Huxtable, at  george@hux.me.uk
or at +44 1865 820222 (from UK, 01865 820222)
or at 1 Sandy Lane, Southmoor, Abingdon, Oxon OX13 5HX, UK.

--~--~---------~--~----~------------~-------~--~----~
Navigation List archive: www.fer3.com/arc
To post, email NavList@fer3.com
To , email NavList-@fer3.com
-~----------~----~----~----~------~----~------~--~---

File:

   

Reply