NavList:

Some threads have been arising in NavList about Running Fix. I will treat to put some light in this issue.

Running Fix is defined as a position determined by crossing LoPs obtained at different times, and advanced or retired to a common instant of time.

First let us start with the true celestial line of position and the generalized problem.

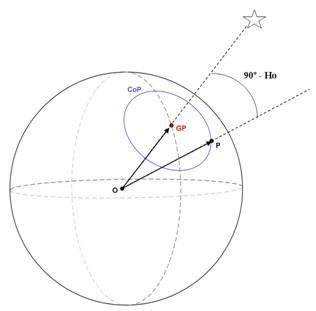
Let OP be the observer’s position at the time of sight, and GP the geographical position of the celestial body at the same instant. The dot product of the vectors defined by the centre of the Earth and these points is the cosine of the angle between them that is the zenith distance of the observed body. The Vector equation of the circle of equal altitude, CoP, is [4]:

Expanding this equation, the best known form of the equation is obtained:

·          B: Latitude N (+) / S (–)

·          L: Longitude E (+) / W (–)

·          GHA: Greenwich Hour Angle. W to E from 0° to 360°.

·          DEC: Declination. N (+) / S (–).

If n observations of the altitude of celestial bodies are made at n times, a set of n equations are obtained:

t1: Ho1 = f( Dec, GHA, B, L )

t2: Ho2 = f( Dec, GHA, B, L )

...

tn: Hon = f( Dec, GHA, B, L )

where Dec, GHA, B, L are also function of time, and position is a function of the motion of the observer during the n observations. In navigation, Rhumb line or GC: (B,L) = f(speed, course). In a 3D space, altitude must be included and the motion could follow a parabolic law, for example in military applications.

Posing the problem with similar methods as in finite element method, (FEM, widely used in engineering, physics and chemistry), the partial differential equations are:

Solving this using a numerical technique for finding the solution, the fix and the parameters of the motion are obtained [1].

For Simultaneous observations, the case is the one described in [3]

There is another method for move a CoP based in two rotations, Metcalf [6]

This is the exact solution for a “running fix”, but of course, it is impracticable at sea/air without the power of a computer. Historical/manual navigation usually advance the CoP or LoP by some techniques, some of them are approximate, because, in fact, the original circumference is deformed in the way of the motion, and these methods assumed that the CoP remains undeformed. Then the solution is only acceptable near the true position:

• In Marcq St. Hilaire intercept method, the point (B,L) from which the line (p,Z) is drawn ,is translated in the same way as with a bearing in coastal navigation.
• Adjust of the altitude [2] [5]  Ho2 =  Ho1 + d * cos(C-Z) = =  Ho + S*(t2-t1) * cos(C-Z)
• Adjust of Dec,GHA [2]

The uncertainty in the knowledge of the real course and speed, due to the wind, currents and steer, is added to the source of error of a sextant measurement.  

Regards,

Andrés Ruiz

Navigational Algorithms

https://sites.google.com/site/navigationalalgorithms/

References:

1. Kaplan, G. H. (1995): "Determining the Position and Motion of a Vessel from Celestial Observations", Navigation, Vol. 42, No. 4, pp. 631-648.
2. http://aa.usno.navy.mil/publications/docs/reports: "The Motion of the Observer in Celestial Navigation". Kaplan, G. H. (1996), Navigator's Newsletter, Issue 51 (Spring 1996), pp. 10-14. PDF (113K) or PostScript (100K).
3. Robert W. Severance. Overdetermined Celestial Fix by Iteration. IoN Vol. 36, No. 4, 1989
4. Vector equation of the circle of equal altitude. Navigational Algorithms. Andrés Ruiz.
5. A Treatise on Nautical Astronomy - John Merrifield”, page 230 http://books.google.com/books?id=WUPCRcglPFkC&lpg=PP1&dq=A%20Treatise%20on%20Nautical%20Astronomy%20-%20John%20Merrifield%E2%80%9D%2C&as_brr=3&hl=es&pg=PA231#v=onepage&q=&f=false
6. Metcalf, T. R. Advancing Celestial Circles of Position, NAVIGATION, Vol. 38, No. 3, Fall 1991, pp 285-288.

• [NavList 11201] http://www.fer3.com/arc/m2.aspx?i=111201&y=200912
• [NavList 10856] http://fer3.com/arc/m2.aspx?i=110856