NavList:
A Community Devoted to the Preservation and Practice of Celestial Navigation and Other Methods of Traditional Wayfinding
From: Frank Reed
Date: 2019 Jan 4, 09:34 -0800
Ed, I don't see any problem. For a lunar distance LD=95°, and body altitude bodyAlt=36°, moon altitude moonAlt=38°, you can calculate the required accuracy in the altitudes from the equations as given (in that post from 14 years ago, notation changed a bit):
AccuracyBody = 6' · sin(LD) / cos(bodyAlt),
AccuracyMoon = 6' · tan(LD) / cos(moonAlt).
You get a required accuracy of about +/-7' for the body altitude and +/-87' for the Moon altitude. Was the negative sign on the Moon required accuracy puzzling you? It's always a "plus or minus" result. The implication is that your altitude for Aldebaran could be wrong by up to 7 minutes of arc and it would not change the result of the clearing computation by more than 0.1 minutes of arc. Similarly an error of as much as +/-1.45 degrees in the Moon's altitude would not change the clearing computation by more than 0.1 minutes of arc. Naturally this is the result of a differential sensitivity calculation, and it assumes linearity by the nature of the mathematics. So you can't take the actual numbers too literally very close to the singularity (90°). In other words, the required accuracy in the Moon's altitude is about 1.5° for this lunar.
The general pattern here is simple. First, short distances:
The 'required accuracy' in the altitudes is approximately proportional to the lunar distance for short distances. Both sine and tangent of any angle are equal to that angle in the small angle limit. For example, suppose both altitudes are about 45° so that the cos terms are both equal to 0.7. Also assume that the LD is small, let's say less than 20°. Then the required accuracy equations reduce to:
AccuracyBody = 6' · sin(LD) / cos(bodyAlt) = 6' · LD / 0.7,
AccuracyMoon = 6' · tan(LD) / cos(moonAlt) = 6' · LD / 0.7,
but these assume LD is a pure angle (or in radians), but for practical thinking it would be easier to work in degrees:
Accuracy = 0.15'·LD°.
Thus if the LD is 10°, you need altitudes of both bodies accurate to +/-1.5' in order to ensure no error in the clearing process. That's a strong requirement, and it's part of the reason that short distance lunars should be avoided. Fortunately, it's easy to show that a common error (for example from an incorrect dip value) has minimal impact.
Next, distances near 90°:
At the other extreme, when the lunar distance is close to 90°, the accuracy requirements diverge radically. sin(LD) settles in at 1.0 while tan(LD) has a singularity --it goes "to infinity"-- right at 90°. That means that the requirement for body altitude stabilizes in this range, but the moon altitudes become insensitive to substantial errors. You can be wrong by a degree or two (or three!) and it may not matter. Why does this happen? Why is there a "ninety degree miracle"? There's really no "clever" reason for this. It's just a cancellation in the math, easy enough to prove mathematically but with no profound significance.
Finally, the sensitivity of the accuracy requirements to the altitudes of the objects is less significant than it may seem. With lunars, we rarely shoot altitudes above 60° because we don't have to. Lunars are not time-sensitive. There's no rush. We can wait for easier geometry, easier sight conditions. In historical practice and in modern experimentation, the altitudes will typically be in the range from 20° to 60°, and in that range 1/cos varies from 1.06 to 2 (or viewing 47° as a "typical" altitude, the impact is only +/-37% in the range from 20° to 60°). This is useful, but it's not "huge".
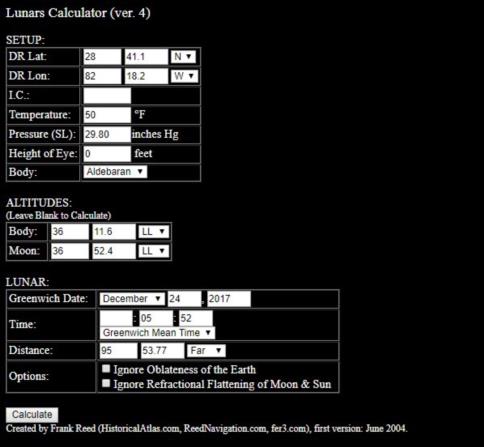
Suppose you want to go beyond the differential sensitivity and analyze a specific case (like this sight data you have posted from Dec.24, 2017). You can do that by direct calculation. Just enter the altitudes and then do some tests. If you increase the Moon's altitude by a degree, what happens to the cleared distance? If you increase the other body's altitude by 6 minutes of arc, what happens? Attached below is a set up for your sight data, slightly modified to give an exact zero error. Enter that data in the clearing calculator web app on my site and see what happens as you adjust the inputs.
Frank Reed