NavList:
A Community Devoted to the Preservation and Practice of Celestial Navigation and Other Methods of Traditional Wayfinding
Re: Winter solstice this weekend
From: Bill B
Date: 2014 Dec 20, 00:39 -0500
From: Bill B
Date: 2014 Dec 20, 00:39 -0500
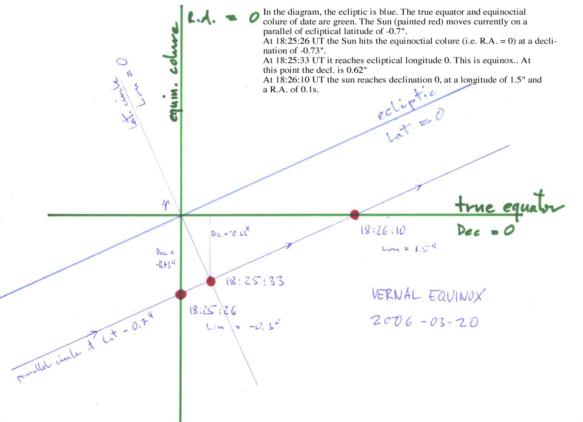
On 12/19/2014 8:36 PM, Peter Hakel wrote: > Depending on your level of patience, you could vary the input UT in the > sun.xls spreadsheet until you reach the most negative declination. To > gain extra precision you can unlock the spreadsheet and display sun’s > Dec with additional decimal digits; in the attached screenshot I copied > this value into the yellow cell E6 from B60. For illustration, I am > showing more decimals in E6 than is reasonable but I wanted to see Dec > changing with every second as a numerical experiment. SNIP > Finding equinoxes this way is easier, since the Dec rate of change is > the fastest and all you need to watch for is the change in sign. For equinoxes, zero declination does not necessarily define the instant of equinox. From years gone by, an explanation and diagram courtesy Herbert Prinz. But before we wade into that, I would love to hear one of our resident astrophysicists expound on the gold standard for a solstice. As promised above: http://fer3.com/arc/m2.aspx/Welcome-Spring-or-Fall-HerbertPrinz-mar-2006-w27802 "Oops! You are some 5 minutes early. The correct value is 18:25:33. If you compute this from the N.A. you should be able to get the time within an accuracy of better than 15 seconds. I don't have a N.A. handy to check it out. In sync with the equinox related traffic that occurs with a period of 0.5 tropical years on this list, I posted a diagram showing the apparent place of the sun around today's equinox with respect to the two fundamental reference frames: http://www.hprinz.us/equinox.jpg In the diagram, the ecliptic is blue. The true equator and equinoctial colure of date are green. The Sun (painted red) moves currently on a parallel of ecliptical latitude of -0.7". At 18:25:26 UT the Sun hits the equinoctial colure (i.e. R.A. = 0) at a declination of -0.73". At 18:25:33 UT it reaches ecliptical longitude 0. This is equinox. At this point the decl. is 0.62" At 18:26:10 UT the sun reaches declination 0, at a longitude of 1.5" and a R.A. of 0.1s. All data computed with MICA Vers. 2, U.S.N.O. Conceptually, equinox implies that the declination of the sun equals zero. Hipparchus supposed this to happen in the equinoctial point, i.e. at zero longitude. When it was realized after Newton that the apparent Sun does not necessarily have to move through the equinoctial point each year, one had to make a decision whether to choose zero longitude or zero declination for the definition of equinox. Longitude was more practical. How come the Sun has latitude? Hint: The latitude of the Sun is always very roughly (give or take 0.2") that of the Moon, divided by 32000. Have fun. Herbert Prinz"