
NavList:
A Community Devoted to the Preservation and Practice of Celestial Navigation and Other Methods of Traditional Wayfinding
From: Frank Reed
Date: 2017 Jan 21, 20:05 -0800
David C, you wrote:
"But I am an old timer stuck in my ways and I use astro. How do I plot my position on the chart? I can use bearings or horizontal angles because these refer to marked positions on the chart. But how do I plot a position referred to the sun, not gps satellites?"
That's what I was getting at in my previous posts. Astronomical latitudes and longitudes can be plotted on a global datum like WGS84 after those coordinates have been corrected for deflection of the vertical.
Any method of true geometric surveying of positions on the globe including visual triangulation, measuring distances with chains and meter sticks, and also ranging methods including GPS, will yield a three-dimensional network of points. It's like you have a "CAD model" of the Earth that includes all the mountains and abyssal depths, all the hills and valleys, nicely laid out in their exact physical relationships to other --a skeletal three-dimensional model of the Earth's surface points. Since the Earth has the topology of a sphere (and is approximately a prolate ellipsoid of revolution), the natural coordinates for plotting that network of points in three dimensions is spherical coordinates projected out from the center of the Earth. That concept of center of the Earth needs to be defined rather carefully, but we'll let someone else worry about that. Picture the globe as transparent with a great lamp at its core surrounded by a perfect mathematical framework defining the coordinate lines of latitude and longitude. The coordinate lines are projected out and they intersect the three-dimensional model that we have built of the Earth's surface. Every point on the Earth's surface then has a uniquely defined pair of latitude and longitude coordinates. And of course, we can also define altitude by meauring each point's distance from the center of the Earth.
Astronomical latitude and longitude work differently. Again we can picture a great lamp at the Earth's center, and that grid of spherical coordinate lines projected outward. But this time we ignore the surface features of the Earth and allow that coordinate projection to run all the way out to the abstract globe of the celestial sphere. From just a few observatories on the Earth, we can map the latitudes and longitudes (in modern terms, the Declinations and Sidereal Hour Angles or Right Ascensions) of every star in the heavens. Then to find the latitude and longitude of any spot down here on the mundane globe, we simply look up. We look straight up to the zenith at that point and then define the latitude and longitude of that point by reading it off from the coordinates we have altready defined on the celestial sphere. That's all celestial navigation does: it reads the coordinates of the zenith from any location on Earth (by observing two altitudes, crossing the circles of position, yada yada yada). Fortunately for us, the gravitational field of the Earth is nearly spherical and has the important property that it is everywhere convex. That means that the zenith of every point on the Earth, at a given instant of time, is uniquely matched to a specific location on the celestial sphere. Every spot on the Earth is matched with a star, maybe a very faint star, that is directly overhead from that spot at a given instant of time.
Notice that these two means of defining latitude and longitude cannot and should not agree. The direction to the zenith at every location on Earth would have to be exactly opposite the precise direction to the center of the Earth in order for that to be true. But the Earth's rotation as well as its equatorial bulge throw that out significantly. If I hang a plumbline at 45° latitude, it will be deflected towards the equator, partly by the centrifugal force from the Earth's rotation and partly by the gravitational pull of that bulge around the equator. The net effect is a tilt of about 11 minutes of arc at that latitude (I may not be remembering the exact number correctly, but it's about that order of magnitude). While this could have been fixed by insisting that all astronomical latitude be corrected by a term approximately equal to 11'·[sin(lat)]2, it was far more sensible historically to change the definition of latitude instead. We use a modified set of coordinates to map the Earth's surface --not actual spherical coordinates, but spheroidal coordinates with a slightly "hacked" definition of latitude. This gets the astronomical latitudes nearly exact over most of the globe.
Locally on scales of dozens to hundreds of miles, there are yet finer variations in the effective gravitational field of the Earth. These are the "deflection of the vertical". If there is a huge mountain range just to the south of your location and a great ocean trench just to the north, then a plumb weight will be attracted by perhaps a minute of arc towards the south shifting the zenith by that same amount to the north. This implies that astronomical latitudes and longitudes will be wrong by that amount compared to proper geometric coordinates. This is not a question of "datum". It's not an arbitrary choice of the coordinate system in use. It's the real difference between astronomical latitude and longitude and geodetic latitude and longitude. Over most of the globe this difference is a couple of seconds of arc or less, but near any significant tectonic features including ocean trenches, great mountain ranges (younger mountains especially), and volcanic islands, there are deflections of the vertical amounting to many seconds and occasionally exceeding one minute of arc.
Frank Reed
ReedNavigation.com
Conanicut Island, New England
Once again for your viewing pleasure, maps of the deflection of the vertical around New Zealand...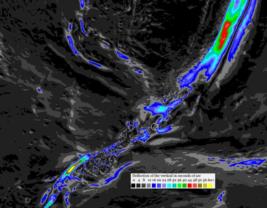
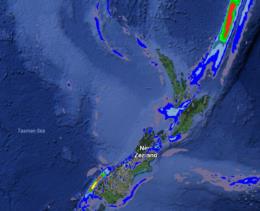
More here if you missed my previous post on this.






