NavList:
A Community Devoted to the Preservation and Practice of Celestial Navigation and Other Methods of Traditional Wayfinding
From: Peter Hakel
Date: 2009 Nov 4, 11:36 -0800
The method consists of the following steps:
1) The LOPs define two planes in 3-D space,
2) The intersection of these two planes defines a straight line in 3-D,
3) The intersections of this straight line with the Earth's surface are the two fixes,
4) Results of Step 3) are translated into latitude and longitude.
The straight line from Step 2) has to be parametrized somehow; and it is the value of that parameter that is extracted in Step 3) from a quadratic equation. There is some freedom in choosing this parameter, which is accompanied by a problem that really cannot be solved within this method, only addressed by an extra step.
I chose this parameter to be the Cartesian coordinate z, which is aligned with the Earth's axis of rotation. This coordinate has therefore a one-to-one correspondence with latitude. If the two celestial bodies are on the same meridian, then the two fixes, while still distinct, have the same latitude, which invalidates Step 3). That is because the straight line from Step 2) is parallel to the equatorial plane (same latitude everywhere). Hence the coordinate z is not a suitable parameter in this case. My spreadsheet handles this issue by testing for the GHA1=GHA2 condition (within some numerical tolerance) and solving the problem in an auxiliary coordinate system rotated by 90 degrees with respect to convention. The solution is then translated back to the original xyz and thus readied for Step 4).
I remember with 99% certainty that Van Allen chose the coordinate x to be this straight-line parameter. With this choice his original method will fail if the two bodies have the same declination, which is precisely the case with my artificial test case. Andres, could this be causing the NaN's you saw? (just trying to make a semi-educated guess here). Perhaps you can detune the GPs a bit and see what happens. If I'm right then moving one GP N/S will eliminate this problem, while moving it E/W will not help.
The Van Allen's method also does not like 90-degree separations in longitude, which can lead to divisions by zero in some cases. My spreadsheet therefore works with its own "Prime Meridian" selected halfway between GHA1 and GHA2. Even then the method will fail when the two bodies are separated by 180 degrees (i.e. sun and full moon) but that is a poor arrangement to begin with and shouldn't be used in the first place.
Finally, a body exactly above a pole (how likely is that? :-) ) also causes a problem; here I went for the easy solution of "detuning" its declination ever so slightly from plus or minus 90 degrees…
To summarize, if I had been aware of John Karl's two-body solution (or better versed in spherical trigonometry to find it myself), I would certainly have used it in lops.xls. A similar observation goes for Andres's clever vector solution. The few caveats we are discussing now are minor compared to the laboriousness of the Van Allen's method. Sometimes (often, in fact) the intuitively clearest approach is not the most practical.
Peter Hakel
From: P H <pmh099@yahoo.com>
To: navlist@fer3.com
Sent: Wed, November 4, 2009 9:21:22 AM
Subject: [NavList 10438] Re: Two-body fix caveat
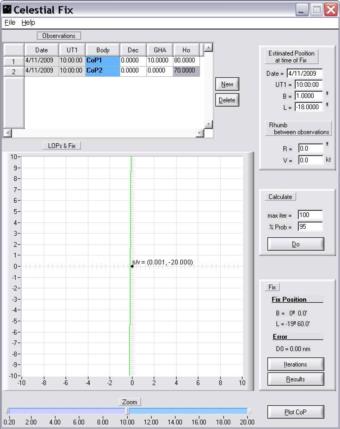
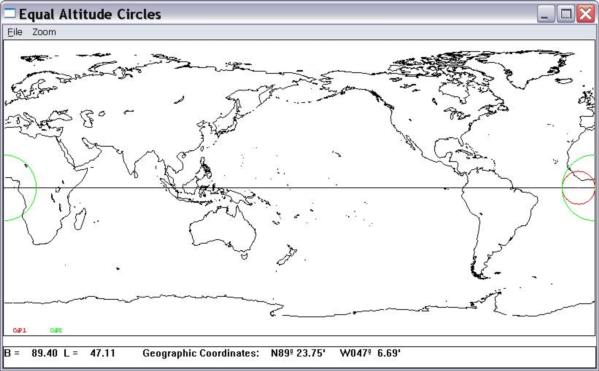
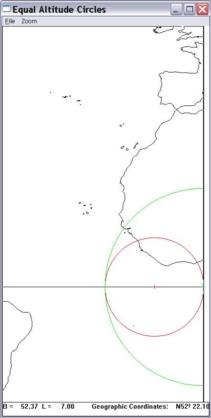
The Van Allen's method works fine for me even in this singular case, see the attached screenshot of the lops.xls spreadsheet.
At the core of this method is a solution of a quadratic equation whose discriminant D, as always, defines three cases:
D>0, two distinct solutions (LOPs intersect, the usual CelNav case)
D=0, one solution (LOPs touch, like in this artificial test case)
D<0, no solution
I was concerned about round-off errors for the D=0 case when I was writing that spreadsheet. If D comes out ever so slightly negative instead of zero, then SQRT(D) has a problem. So far, however, Excel numerics has passed all such tests OK, including this one.
Peter Hakel
From: Andres Ruiz <aruiz@orona.es>
To: navlist@fer3.com
Sent: Wed, November 4, 2009 2:12:28 AM
Subject: [NavList 10426] Re: Two-body fix caveat
Solving this singular case with Van Allen’s method: no solution. Vector Solution works fine.
An analytical solution of the two star sight problem of celestial navigation
James A. Van Allen. NAVIGATION Vol. 28, No. 1, 1981
iter Err Be Le B1 L1 B2 L2 GHA1f dec1f GHA2f dec2f
0 NaN NaN NaN NaN NaN NaN NaN 10.000000 0.000010 0.000000 -0.000010
I1: NaN NaN
I2: NaN NaN
Vector Solution for the Intersection of two Circles of Equal Altitude
THE JOURNAL OF NAVIGATION (2008), 61, 355-365. The Royal Institute of Navigation
Andrés Ruiz González - Navigational Algorithms - http://sites.google.com/site/navigationalalgorithms/
iter Err Be Le B1 L1 B2 L2 GHA1f dec1f GHA2f dec2f
0 134.146176409012696 0.000058 -20.000000 0.000058 -20.000000 0.000001 -20.000000 10.000000 0.000010 0.000000 -0.000010
I1: 0.00000 -20.000000
I2: 0.00000 -20.000000
Andrés Ruiz
Navigational Algorithms
http://sites.google.com/site/navigationalalgorithms/
--~--~---------~--~----~------------~-------~--~----~
NavList message boards: www.fer3.com/arc
Or post by email to: NavList@fer3.com
To , email NavList+@fer3.com
-~----------~----~----~----~------~----~------~--~---