NavList:

As many of you know, I teach a class in "Celestial Navigation: 19th Century Methods" which covers the "Old Navigation" (latitude by Noon Sun, longitude by time sight). With the discussion of Martelli's time sight tables, I thought it might be worth talking a little more about the basic principle of the time sight.

The time sight was the preferred sight for finding longitude for nearly two centuries. If you have GMT from some source, either a chronometer, or a watch set by a recent radio time check, or even a lunar, then you can get longitude by comparing Greenwich time with the local time. The difference in hours, converts to degrees of longitude at the usual rate of 15 degrees per hour. So if it's 11:59pm on Christmas Eve in Greenwich, and we check the local time in St. Louis, Missouri and find it's 5:59pm then that's six hours or 90 degrees of longitude difference. Easy as could be.

To get local time, we can use a sundial. That's what we're talking about when we refer to local time. It's really local apparent time, the time that a sundial reads. Sundials are fine on land but not much use on a ship since they have to be level and oriented correctly. Even on land since a shadow cast by the Sun has a fringe of about half a degree, a sundial can only be read reliably to the nearest minute of time or so. We can do better by measuring the Sun's altitude with a sextant. Then by calculation we can convert that altitude into the local apparent time. It's easy to see how this would work if you consider the special case of the Sun on an equinox as seen from the equator. At the equator on an equinox, the Sun claimbs straight up from the horizon, due East, and its altitude (corrected for IC, dip, SD, ref.) immediately gives the time. When the corrected altitude is zero at sunrise, the time is 6:00AM. When the altitude is 15 degrees, it's 7:00AM; 30 degrees, 8:00AM, and so on. With a little spherical trig, and knowing the Sun's declination and our latitude, we can work out the rules for all other cases. The key concept here is that we are using the sextant as a glorified sundial. And in fact, on land we can check our work by comparing the calculated time with the time indicated by a properly installed sundial.

When comparing local apparent time with the time displayed by a proper clock, we need to convert from apparent time to mean time. That conversion is the value of the "equation of time" (which is not an equation in the sense of algebra; rather it's an archaic meaning of 'equation' which we might translate as 'equalizer of time' or 'corrector of time'). The Equation of Time was formerly just as important as the Declination in almanacs for navigators. Today this is hidden in the Sun's GHA (they do include the daily value of he EqT at the foot of the Nautical Almanac's pages today, but that's not accurate enough except for planning purposes). Historically, a navigator would take out the Dec and the EqT for the Sun together from whatever almanac was available.

As for the calculation itself, since I'm short on time at the moment, I'm just going to cut and paste some brief instructions from the tables I publish for my class.
"LONGITUDE BY TIME SIGHT, 19th Century:
-Measure altitude of Sun LL (Lower Limb) when bearing East or West. Record exact GMT at that instant.
-Apply IC (index correction) to altitude. Add 12'.
[12' is a "mean" correction for dip+SD+ref. If you choose, you can improve on this]
-Get Sun's Declination (interpolated by hour of GMT).
[from an almanac or equiv.]
-Estimate Latitude by dead reckoning from last known position.
--Get Sun's "polar distance": pd = 90 +/- Dec.
[Sun'd angular distance from the "elevated pole"]
--Calculate the "Half Sum": hSum = (Alt + pd + Lat)/2
--Calculate the "Remainder": Rem = hSum - Alt
--Add up four logarithms from tables: Rem, pd, Lat, hSum.
--"Reject the tens" from the Total of the logarithms. Divide by two. Call it hT.
[for "half Total"]
--Find Time in tables corresponding to hT.
[selecting A.M. or P.M. by observation -you know when you took the sights]
-Adjust for Equation of Time for that date (interpolated by hour of GMT).
[from almanac or equiv.]
-Result is Local Mean Time. Subtract LMT from GMT.
-Result is Longitude as time. Convert time to degrees."

In the steps above, lines preceded by two dashes (--) are specific to this method. Other steps would apply to any method of working a time sight, including, for example, Martelli's.

Note that the logarithm tables that I publish for my class are quite brief. Almanac data plus logarithm tables plus short instructions amounts to only 30 pages (15 double-sided). That's all you need to cross an ocean using the "Old Navigation" if you only take Sun sights. And the tables are good for at least 12 years into the future.

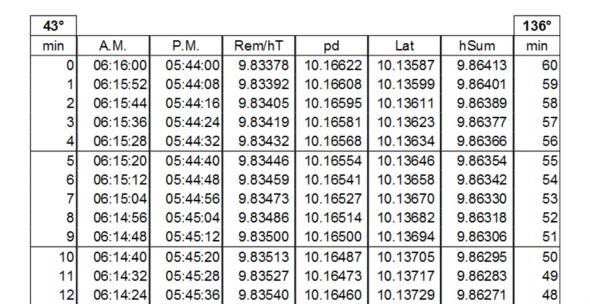
I'm attaching a sample from the log tables that I use for this class. The only slightly modern variation is that they're given headings corresponding to the argument rather than the trig function. Beyond that, they're just standard log trig tables. They're so short because they are designed to be entered from any corner of the page. It's confusing at first but a great savings in pages.

-FER

----------------------------------------------------------------
NavList message boards and member settings: www.fer3.com/NavList
Members may optionally receive posts by email.
To cancel email delivery, send a message to NoMail[at]fer3.com
----------------------------------------------------------------