NavList:
A Community Devoted to the Preservation and Practice of Celestial Navigation and Other Methods of Traditional Wayfinding
From: Gary LaPook
Date: 2010 Dec 9, 12:31 -0800
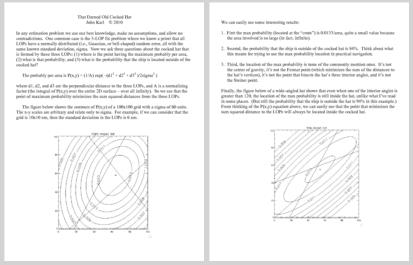
| There are four methods recommended for finding the spot inside the cocked hat that you can choose to represent the fix. First, just visually estimating the spot. Second, find the midpoint of each LOP and draw a line from each midpoint to the opposite angle, their intersection is the fix. Third, draw the bisector of each corner angle and their intersection marks the fix. And fourth, the Steiner point. See the diagram I had previously uploaded at: http://www.fer3.com/arc/imgx/FM-30-476.pdf (The bisector method is illustrated in Bowditch, 1938 and in Dutton, 1926.) I have also used 2/3 of the length of the line connecting the midpoint to the opposite angle as another way to determine the fix using the midpoint method. I am attaching several drawings showing each of these methods for comparison. The first shows a 90-45-45 triangle showing the Steiner point which is labeled as "A" in the drawings. Next is the same triangle with the midpoint method locating the fix marked as "B". Next are a series showing a simple way to find the 2/3rds point method of finding the fix. With a dividers measure the length of the line. Next put the dividers on a line drawn at 48 degrees (which has a cosine of .66)and swing the point to the vertical line and you automatically have 2/3rds. (You will also notice that there is another line drawn at 60 degrees which I used to divide the lengths of the LOPs by 2 for finding the midpoints using the same procedure.) Then place the dividers at the angle and you will see that this determines the same fix as the midpoint method. Last is the fix determined by bisecting each angle and this fix is marked as "C." You can take your choice as which point is the best to use for the fix. I have also attached a similar series for a 90-70-20 triangle like the one in your original post. You can also see that the 2/3rds method works from each of the angles. If you compare this final drawing with Karl's original diagram http://www.fer3.com/arc/imgx/Darned-Old-Cocked-Hat.pdf his plus mark is closest to the Steiner point. Although his plus mark is the highest probability point at .0133 all three methods produce a fix within his .013 contour so there is not much reason to choose one point over the other in using any of these methods. gl --- On Wed, 12/8/10, John Karl <jhkarl@att.net> wrote:
|