NavList:
A Community Devoted to the Preservation and Practice of Celestial Navigation and Other Methods of Traditional Wayfinding
From: Frank Reed
Date: 2021 May 30, 16:02 -0700
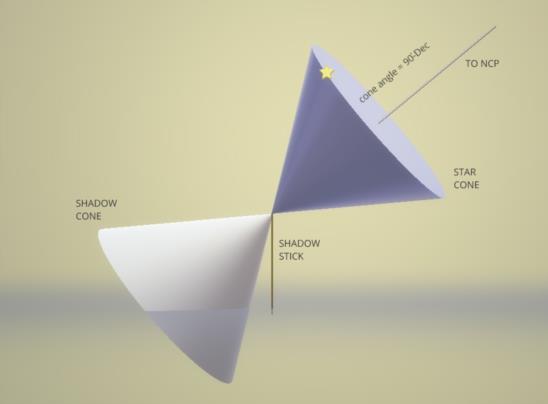
A star travels around the sky on a small circle, unless the star has exactly zero declination. We can draw a ray from the top of that stick that we hammered into the ground to the star, and in the course of the day the star will travel around that small circle, and the ray will sweep out a cone with its apex at the tip of the stick. The central axis of the cone points to the celestial pole. In the case I've drawn below, it's the north celestial pole (NCP). The angle from the axis of the cone to the star at any time (the radius of the small circle or the apex angle of the cone) is 90°-Dec.
Extend the ray from the tip of the shadow stick down the ground. That's where the shadow of the tip of the stick is created by my imaginary "Vega supernova". During the course of a day, the shadow ray will move in lockstep with the ray to Vega creating a second cone, a shadow cone. That shadow cone intersects the ground which we assume is a flat plane. Cone intersects flat plane... What do you get? Conic sections... of course! So that means that the shadow of the tip of the stick will trace out a circle, or an ellipse, or a parabola, or a hyperbola.
If the observer is at the geographic pole so that the celestial pole is straight up, then the cones have their axes vertically aligned, and the shadow cone intersects symmetrically. The shadow is a circle. Makes sense. If you're at the north pole watching Vega, it travels around the sky at a fixed angular altitude equal to its Declination, so the shadow from the stick will sweep around in a circle during a single sidereal day.
When would you get a perfect parabolic shadow curve?
Frank Reed