NavList:
A Community Devoted to the Preservation and Practice of Celestial Navigation and Other Methods of Traditional Wayfinding
From: Frank Reed
Date: 2021 Jun 1, 10:46 -0700
Yes. There are four classic conic sections, right? Circle, ellipse, parabola, hyperbola. We can also extend this list and add point and straight line as special cases. Of course we could go the other way and shorten the list to ellipse and hyperbola only since the others are unique cases that occur only under mathematically exact circumstances. In any practical case that looks like a circle or a parabola, if we measure closely enough, we will find that we "really" have an ellipse or hyperbola (or we have broken the limits of the analysis in some other way... celestial objects don't have fixed declinations, the ground is not a perfect plane, etc.). Nonetheless the perfect cases are important conceptually.
If I stand at the north pole and watch Vega through the course of a sidereal day, it traces out a small circle with a radius equal to 90°-dec or 51.2°. The shadow path on the ground is a circle. As I walk away from the pole, the path becomes an ellipse. The dimensions of the ellipse are not too difficult to calculate.
There comes a point where the ellipse doesn't quite close. This happens when the star just barely touches the horizon in the north (staying north-focused in this analysis for now). As long as Vega is circumpolar at our latitude, the shadow is an ellipse. But as soon as we reach the latitude where it skims the horizon in the north, the ellipse no longer closes. As with all limiting cases, it's a bit "weird" to ponder! This is the parabolic case. It's a dividing lilne among the cases. In terms of the geometry of the cones, the low side of the star cone in my picture and the high side of the shadow cone would be exactly horizontal in this case. And that's just what's required by the definition of a parabola: the side of the cone is exactly parallel to the intersecting plane.
For lower latitudes the cones are tilted at higher angles, and the intersections with the horizontal plane generate a series of hyperbolas.
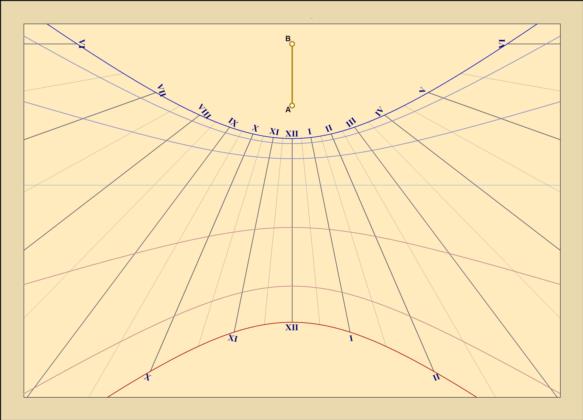
We've all seen a variation on this family of hyperbolas. The case where we vary the declination at a constant latitude is often displayed on sundials (see below). These curves on sundials seem to create a calendar to accompany the usual clock function of the dial, but the resolution of the calendar is poor so in truth these curves are decorations --"geeky" decorations. Each curve corresponds to a date (or pair of dates in different seasons). For mid-latitudes the curves are hyperbolas except in one degenerate case. If the declination is zero, then the angle inside the star cone and the matching shadow cone is 90°. In that case the two cones open out to become two coinciding flat planes, and the intersection with the horizontal plane is a straight line. This is the equinox case. On the equinox, or for any celestial body with a declination of 0°, the Sun or other body rises exactly due east, sets due west, and travels during the day along half of a great circle. That great circle, the tip of the shadow stick, and the path of the shadow on the ground all lie in one plane, and therefore the intersection with the ground plane is a straight line.
Some details: how does the path change when refraction is included? How does the Sun's path change when we include the daily change in its declination?
In the images below, the old sundial is one of my favorites. It's currently located outside a restaurant in Rome. The diagram of hyperbolic curves is generated by a very nice "dialing" app called Shadows Pro which I recommend (Windows only).
Frank Reed
Clockwork Mapping / ReedNavigation.com
Conanicut Island USA