NavList:
A Community Devoted to the Preservation and Practice of Celestial Navigation and Other Methods of Traditional Wayfinding
From: Robert Bernecky
Date: 2016 Jan 23, 08:28 -0800
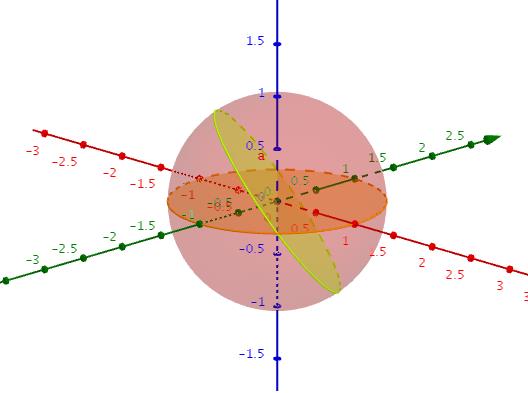
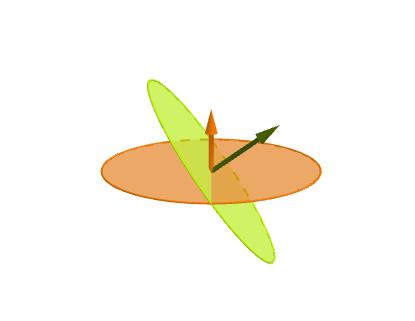
In case it is not clear, all the "lines" on the sphere are great circles. A great circle has its center at the center of the sphere and its circumference on the sphere. See attached for examples. (note that latitudes are not great circles, but longitude lines are.) The angle that two great circles make with each other can be thought of in this way: put an arrow at the center of the great circle so that it points perpendicular to the surface of the circle. Do that for the other circle. The angle that the perpendiculars make with each other is the angle that the great circles make with each other. The green and orange arrows in the 2nd figure are an example.
For your problem, create a triangle using e.g. the north pole, the start point and the finish point of your route, and connect the dots. Then pick (for example) the start point and "drop a perpendicular" to the opposite side (formed by the great circle from the north pole to the finish point). This "perpendicular" is a great circle that goes through the start point and whos "arrow" (at the center of the earth) is 90 degrees to the arrow of the great circle that goes through the north pole and finish point.
Depending on whether the start point is north or south of the finish point, the perpendicular may be "outside" of the orginal triangle. Things still work, but working out the details can take some time.
As an example, see the write up on how the Nautical Almanac's Concise Reduction Table "works" (at least for one case). You can ignore the 2nd part dealing with corrections.