NavList:

   

Reply

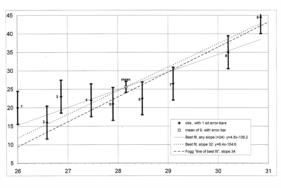
I wish to return to Peter Hakel's posting of 3 Jan.

I had written, on 2 Jan,

"You seem to have ended up with a best-fit slope of about 24' in a 5-minute
period, as I did when allowing Excel to make a best-fit, when giving it
freedom to alter the slope as it thought fit. But the slope can be
pre-assessed with sufficient accuracy from known information, and unless
there is some error in the information given, such as an (unlikely) star
mis-identification, we can be sure that the actual slope is nearer to 32',
and the apparent lower figure is no more than a product of scatter in the
data. This is a point that Peter Fogg keeps reiterating, perhaps the only
valid point in all he has written on this topic."

To which he replied-

"Precomputing the slope requires DR information, which I chose to avoid 
using at the very beginning."

=======

But why do so? That's the whole point of this exercise, that in some cases 
the slope can be rather accurately pre-assessed, rather than derived from a 
rather poor set of data.

In this case, the altitude of the star had been measured to be around 66º 
30'. It's unlikely that the star had been misidentified, as Canopus is the 
brightest thing in that patch of sky, by quite a long way, its declination 
being 52º 42' S. The only other quantity that affects the slope is the 
observer's latitude, which I suggest we can take as well-known in this 
case, being right on the doorstep of the home-port of Sydney Harbour, at 
34ºS. Taken together, these give rise to a slope of around 32' over 5 
minutes.

But Peter Hakel's computer assessment, when allowed free rein to choose its 
slope arrives at a slope of 24' over 5 minutes. To arrive at such a slope, 
the observation would have to be taken from a latitude of 31º 40' S, or 
thereabouts, being about 150 miles North of Sydney Harbour. That seems 
highly implausible.

So let's have a look at the data that Peter Hakel's estimate was based on, 
in the attachment. I would agree that the better fit, with no other 
information to go on than those plotted point, would be the continuous line 
at a slope of 24. Peter's program says so, an Excel fit says so, and my eye 
says so. But is the dotted line, which is constrained to have a slope of 
32, in any way actually INCOMPATIBLE with those 9 data points, with all 
their scatter?  Not at all! If that dotted line represented the real truth, 
then those 9 points, would represent a perfectly plausible set of data, 
about that line.

Asked to assess the slope, I would trust the observer's stated latitude, 
then, rather than the attempt to fit a slope to those widely-scattered data 
points. I suggest that Peter Hakel is allowing the computational 
mathematics to seduce him away from the commonsense of the real problem.

Not that it matters, much. Because we have shown than the mean point (mean 
time, mean altitude) represents just as good a fit, whatever the assumed 
slope of the line.

George.

contact George Huxtable, at  george@hux.me.uk
or at +44 1865 820222 (from UK, 01865 820222)
or at 1 Sandy Lane, Southmoor, Abingdon, Oxon OX13 5HX, UK. 

File:

   

Reply