NavList:
A Community Devoted to the Preservation and Practice of Celestial Navigation and Other Methods of Traditional Wayfinding
From: Frank Reed
Date: 2020 May 20, 11:54 -0700
In fact, you can understand a large fraction of the iso-azimuth shapes (with major exceptions!) in a very simple way, so long as the other point is not too close to the equator. Draw the ordinary diagram for horizontal sextant angles between two lighthouses where one "lighthouse" is now the north pole and the other "lighthouse" is the sub-star point of the celestial body. These are circles, of course (see PS). I previously wondered if these might map directly onto small circles on the globe in the full 3D case. This is definitely wrong in the general case, but it also certainly true "in the limit" of small circles. For example, if the star is Polaris, so that the polar distance is only 40 nautical miles, then the difference between the iso-azimuth curves on the sphere and in the plane (equivalent to horizontal sextant angles) is negligible, unmeasurable.
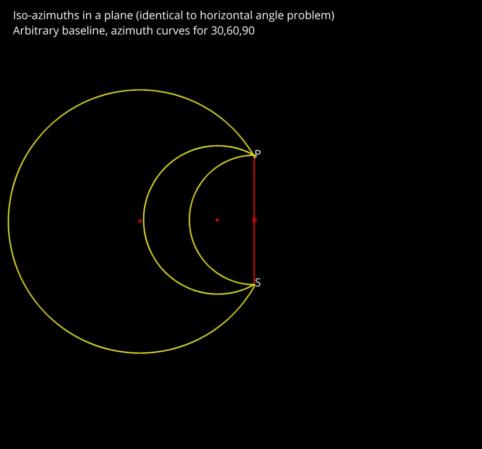
It's interesting, and certainly useful for visualization, that the horizontal case extends to substantial distances from the pole as a good approximation. Draw the plane case. Then drop that onto a projection of the globe seen from above the mid-way point between the pole and the sub-star point. The circles are almost a perfect match for iso-azimuths from about 45° to 180° (and similar angles on the other side by symmetry). These circles when plotted in three dimensions on the globe "droop down" and create the exotic shapes that you'll see in many cases.
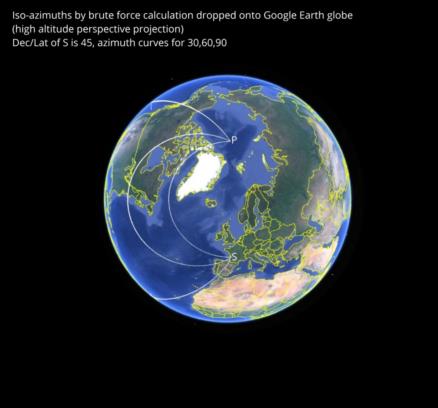
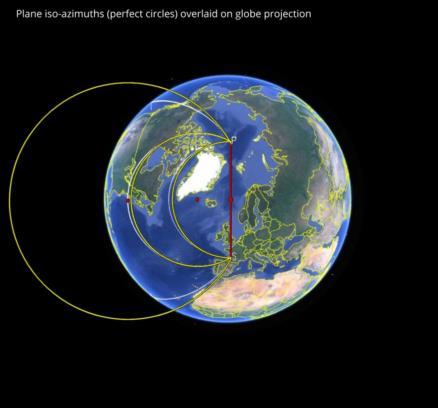
In the images below, we can see the iso-azimuth curves by "brute force" calculation. I simply calculated the azimuth at every point on the globe and kept those points within a small tolerance of the target azimuth for each curve. Displayed in Google Earth, these curves look approximately like circles when viewed from high altitude above the mid-point between the sub-star point and the pole (this is a simple "perspective projection" or "bird's eye view" in Google Earth which tends towards an orthogonal projection as the view point climbs to high "orbital" altitudes. Next I have drawn the iso-azimuths for the plane case. Then we can pick up the plane case and superimpose it on the projected "view from above". It's a very close match for the two smaller circles (iso-azimuths for 60°, 90°) but only qualitatively for 30°.
The projected "view from above" implies that the circles as drawn are really cylinders intersecting the spherical globe, and when we look at the curves from a point above the tropics, we see that they "droop" where the cylinders cut the globe. The curves on the surface are not in flat planes. But the appearance from above can be easily sketched in many cases, and that's a nice feature. Draw a circle, like a common horizontal sextant problem, then project on the globe.
By the way, I'm just showing you what I have so far in this story. It's quite possible that there's a better projection that makes this more interesting for visualization. It's also possible that this is as good as it gets. However you look at it, this approach provides an easy way to visualize the iso-azimuths in a large fraction of cases. They are circular arcs when seen from high above the globe.
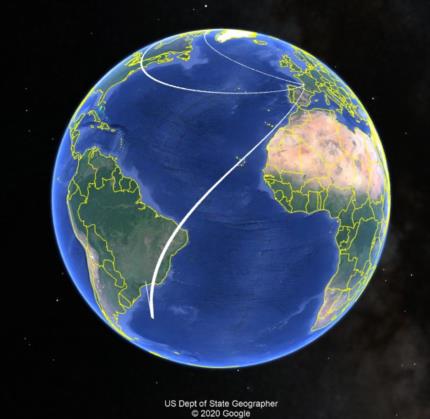
Looking for a big exception to all of this? Consider Mintaka seen exactly due east. And let's round Mintaka's Declination so that it is exactly zero. Further, let's pick a date and time so that the GHA of Mintaka is also zero. That places the sub-star point on the equator and on the prime meridian (a bit south of Ghana). Where can this star be seen exactly due east? Well, clearly at all points on the equator west of Ghana up to 90° west longitude. But also at every point at all latitudes along the meridian of 90° west longitude, the azimuth will also be due east. The iso-azimuth in this case is two great circle arcs intersecting at a right angle (in the Galapagos Islands). This appears to be the most extreme case.
Frank Reed
PS: if you have never encountered the problem of circles of position from horizontal sextant angles, you should look it up and understand that first. None of the above will make sense without that basic background. The most basic case is a circle centered on the mid-point between two lighthouses. The circle has a radius equal to the distance from the mid-point to each lighthouse so that both lighthouses sit on opposite sides of the circle. Everywhere along that circle, the relative bearing (difference in azimuth) between the two lighthouses is exactly 90°. If you measure an angle between them of 90°, then you must be somewhere along that circular arc. Note that if you can distinguish one lighthouse from the other, you can only be on one side of the circle. For differences in azimuth less than 90°, the center is offset to your side of the baseline, and the portion of the circle where you could be located is enlarged as in the "plane case" diagram attached here.