NavList:
A Community Devoted to the Preservation and Practice of Celestial Navigation and Other Methods of Traditional Wayfinding
From: Frank Reed
Date: 2020 May 18, 14:11 -0700
Are the iso-azimuths small circles? Is it just the plane projection that makes them look so exotic?
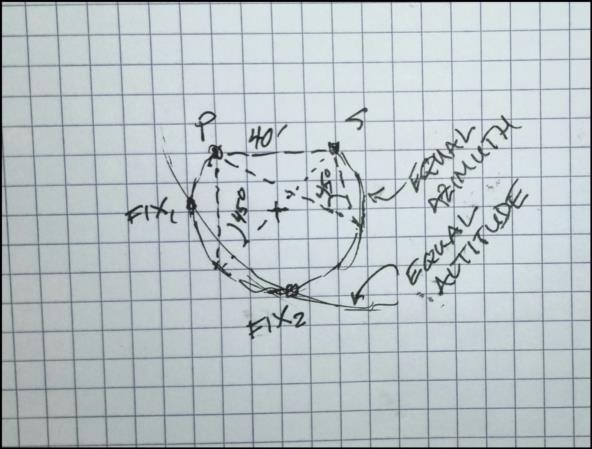
Consider the case of Polaris. Suppose I measure its altitude to be 89°10' and I measure its azimuth to be 45°00'. Let's make the pd (co-Dec) of Polaris 40' exactly, close to what it has been recently. I can now draw two circles: one is the usual circle of position with a radius of 50 n.m. centered on the subStar point of Polaris, call it S, which is 40 n.m. from the pole, call it P. Next I can draw a circle of constant azimuth (this is exactly equivalent to a circle from a horizontal sextant angle ...imagine P and S are lighthouses). Note that a portion of the circle is excluded since it doesn't have the right azimuth. For an azimuth of 45°, the geometry of the circle is relatively simple. It is centered on a point on a line perpendicular to the line from the P to S. The distance of the center off the line is 20 n.m. It's radius is 20·sqrt(2) or roughly 28 n.m. The standard circle of equal altitude cuts the circle of equal azimuth in two points. We can see that there will be two solutions when the zenith distance is greater than the polar distance so long as the azimuth is less than 90°. Other conditions in other cases.
Does this small distance approximation extend to the complete spherical case? Is the equal azimuth curve in the general case simply a small circle (with a segment excluded, as above) hiding in the tall grass of cartograhic projections? I suspect that's the case. If so, what are its properties? Where is the center of the circle in the general case? What is its radius?
Frank Reed