NavList:

   

Reply

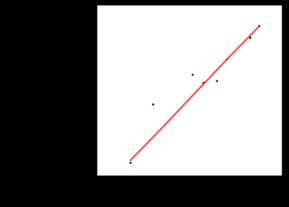
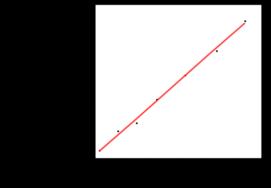
On Dec 23, 2003, at 6:56 AM, George Huxtable wrote:

> Fred Hebart wrote-
>
>> On thinking on this a bit more, I believe that to _rate_ a chronometer
>> one needs at least three lunars spread over at least three days.  In
>> that procedure, one is looking for the rate of change of chronometer
>> time relative to astronomic time, as well as the absolute departure.
>> Then one would regress clock time on astronomic time and look for
>> significant departures from 1.0 in the slope.  This would not be
>> possible over a series of sights _within_ one lunar, such as over a
>> period of one hour, because the clock error would be negligible on any
>> chronometer worth winding.
>
> Comment from George.
>
> I'm not sure why Fred insists on three such observations rather than
> two, but I doubt if it will help much.

I was insisting on three observations because one can always fit a line
to two points; one would not know how good the fit was with only two.


>
> Rating a chronometer involves comparing it with a precise astronomical
> clock, to a fraction of a second, over at least one day, preferably
> several
> days. Or with a noonday gun, or with precise time-sights of a celestial
> body from a known fixed location. The important thing is that these
> times
> should be known to a second, or preferably less, and applied over a
> prolonged period. Let's presume we can check the rate of a chronometer
> to
> within one second per day, and rely on that rate to remain constant
> (which
> is the test of a good timekeeper). After a two-month ocean passage
> (common
> in those days), at the ensuing landfall it might well be a minute out
> in
> time. At that stage, it's timing accuracy would not be much better than
> that of a lunar. That's why an accurately measured rate (and a constant
> one) is such an important matter.

   One might not be able to rate a chronometer to the second using
lunars, but it could be rated to the minute, or about 30 seconds in the
hands of a good practitioner.

>> So a regression of distance on clock time is not needed to reduce the
>> observations from a single lunar.  It can be one relatively simple
>> method (using a computer) of drawing a line through the observations
>> to
>> check for outliers and to assess how scattered the data are.  If a
>> point falls conveniently close to the line near the middle of the
>> observations, it would be a reasonable one to clear.
>
> In my view, the ONLY purpose in making a plot of lunar distance against
> time is to show up blunders, points so far off the trend-line as to
> show
> that something has gone significantly wrong. That's valuable
> information,
> allowing such points to be eliminated.

As well as detecting single blunders, one can also get an idea of the
quality of the observations (I suppose this would be equivalent to
detecting multiple blunders!).  To illustrate this, here are two
lunars,  one of low to moderate quality (mine) and one of fairly high
quality (Frank Reed's).


Moon, Sun, Fred Hebard 36d46.8'N 81d50.7'W


time of last tick on x-axis is 18:36:40.  Time of first tick is 18:20:00


Moon, Jupiter, Frank Reed 41d22'N 71d57'W


time of last tick on x-axis is 09:55.  Time of first tick is 09:30


>
> Certainly one COULD plot a line calculated from a least-squares fit,
> but I
> doubt if it would add anything useful to the simple process of
> averaging
> the lunar distances and the times. Alternatively, a line of best-fit,
> drawn
> with judgment by eye, could be used. In either case, the combination of
> time and lunar-distance, given by ANY point lying on that line,
> preferably
> near its middle, can be used for the purpose of calculation. Presuming
> that
> altitudes of Moon and other-body had been measured rather than
> calculated,
> perhaps the best point to choose along that line would correspond to
> the
> mean time of those altitude observations.
>
> I take it that instead of choosing a point on that line, Fred was
> making
> his reductions based on a single observation that he observed to lie
> very
> close to that line of best fit, not from a point on that line itself.
> If
> so, he could do better.

The main point of my original post was that the first observation of
Frank Reed's is smack dab on the regression line, but it is not as good
as the one taken a bit after 9:42:30.  With a regression line, it is
important that a point near the middle of the line be chosen, and, in
general, averaging is much better than these graphical methods for
determining the time.  I believe George is making the same point.

I was essentially substituting a regression line for a line of best
fit, drawn by eye, since that line is but a button push away with the
software I use; I regard it as more-or-less equivalent to the line of
best fit drawn by eye.

>
> In these circumstances, I regard the benefits of modern statistical
> analysis (least-squares-fits and such) as largely illusory, even if a
> computer can make such calculations so easily.. Which is similar to the
> message that Herbert Prinz was putting across, when he said it was
> "shooting with guns at sparrows".

I agree.  However, the "modern" statistical analysis was actually
invented by Gauss and Laplace (Legendre?) to analyse data such as
these.

I was also trying to extend this post to how one would rate a
chronometer.  I am curious about the statistical procedures used for
these high-quality physical data.

Fred Hebard

File:

File:

   

Reply