NavList:
A Community Devoted to the Preservation and Practice of Celestial Navigation and Other Methods of Traditional Wayfinding
From: David Pike
Date: 2022 Sep 6, 16:02 -0700
Concluding Lesson
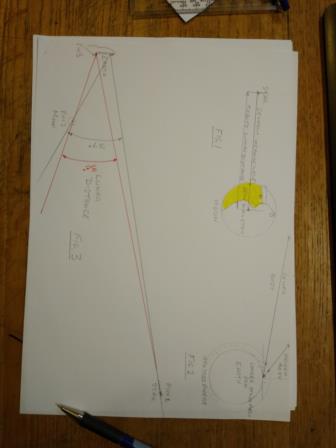
Need I go on? In lesson 4 I was going to point out that lunar distance tables give the angular differences between the centres of the bodies so: Q. How do you aim at the centre of the Moon with sufficient accuracy? A. Aim at the edge of the Moon in line with the chosen star and add or subtract the Moon’s semi-diameter (Fig 1).
Then I would explain that light from a celestial body is bent towards the Earth as it passes though the Earth’s atmosphere so: Q. Which light beam would pass through most atmosphere, light from a body high in the sky, or light from a body low in the sky? A. The light from the lower body (Fig 2). Q. So, if the Moon and the chosen Star are not at the same altitude in the sky, what additional correction are we going to have to apply? A. A correction for difference in atmospheric refraction.
Next, I would demonstrate parallax. Give the students a sheet of A4 paper and three pins. They should mark a short line along the left-hand edge of the paper, this is the Earth, and position one pin somewhere along the right-hand side. This is the selected star. Then get them to put the second pin somewhere on the paper much closer to the left-hand edge that the right-hand edge. This is the Moon. Next, they should place their third pin at one end of the Earth line they’ve drawn and mark in the lines of sight to the Moon and the star. After that, do the same with the third pin placed at the opposite end of the Earth line (Fig 3). Then, they should measure the angles between the star and the Moon from each end of the Earth line. Hopefully they will have recognised the effect of parallax and will understand the need to do something about it. What do they say? “Tell me and I forget. Show me and I remember. Let me try it myself and I’ll understand”.
I was hoping that a lunar distance expert would have taken over by now, as indeed a few of you have, so I’m going to dip out here. All I’ll say is that having taught pupils ages 11 to 18 a myriad of subjects ranging from Special Needs Maths and Science to A Level Design and Technology in an English Comprehensive School from 1982 to 1997 (Well, RAF Navigators are supposed to be able to teach anybody anything; aren’t they?) before escaping back to the RAF for a rest, you have to take things slowly and allow the students to work things out for themselves, or you’ll lose them. DaveP