NavList:
A Community Devoted to the Preservation and Practice of Celestial Navigation and Other Methods of Traditional Wayfinding
Re: Logarithms by Hand
From: Hanno Ix
Date: 2014 Jun 8, 15:15 -0700
From: Hanno Ix
Date: 2014 Jun 8, 15:15 -0700
Peter,
There are not many who can execute that much arithmetic in 10 min - including me.
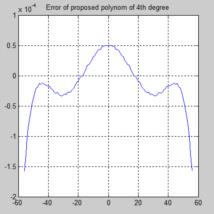
Therefore I tried to find a 4th degree polynomial fitting cos(x) for x = - 45 to 45 deg. As you said, angles from outside this range can be handled by symmetry. According to past experience I judge an error of less than + / - 10^-4 as acceptable for CelNav. I hope you agree.
To make calculations by hand simple my goals for the polynomial were:
To make calculations by hand simple my goals for the polynomial were:
- calculating with degrees in decimal form such as 12.34 deg.
- coefficients with a small number of digits < > 0.
- easy digits such as 1, 2, 5 in the coefficients.
- repetitions of the digits in the coefficients.
- carrying not more than 4 digits in the powers of x
A polynomial with the following coefficients seems to fit the bill:
c4= 3.7e-9;
c3 = 0;
c3 = 0;
c2 = -1.521e-4;
c1 = 0;
c0 = 1 - 5e-5;
There are just 5 digits < >0 in the coefficients: 1, 2 ,3, 5, 7.
This will simplify the multiplications. Unfortunately, there are
no repetitions of digits other than the 1. And I don't like the digits 3 and 7.
This will simplify the multiplications. Unfortunately, there are
no repetitions of digits other than the 1. And I don't like the digits 3 and 7.
However, the most work for the evaluation is in x^2 and x^4;
The polynomial will then be: F(x) = c4*x^4 + c^2*x^2 + 1 - 5e-5;
The error of F(x) versus the the true values cos(x) is depicted in the attached graph.
The evaluation and the graph was done by MATLAB, not by hand, though.
Hanno
On Fri, Jun 6, 2014 at 7:26 PM, Peter Monta <NoReply_PeterMonta@fer3.com> wrote:
Here's a hand-worked four-place sine/cosine (attached). Takes around 10 minutes, so for a sight reduction with three of these, plus an arcsine and arctangent, plus a few additional multiplies and adds, you're looking at something like an hour.
If one needs to do a lot of these, it might be better to precompute a small table every 5 degrees or so, then use a lower-order method.The angle shown is near the upper end of the 45-degree interval to illustrate the need for all the terms. Angles outside of 0..45 degrees can be handled by symmetry.The check is really essential---I tried several of these and made arithmetic blunders on about half of them. Also writing out the partial products in full and not propagating carries until the end (unlike the method taught in grade school) seems to give better reliability. If working to more places, omitting many of the low-order partial products cuts the time in half.
Cheers,PeterAttached File:
(img/127936.trig.jpg: Open and save)