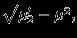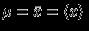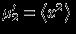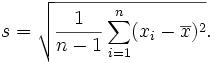NavList:
A Community Devoted to the Preservation and Practice of Celestial Navigation and Other Methods of Traditional Wayfinding
From: Gary LaPook
Date: 2005 Apr 20, 14:24 -0700
The standard deviation of a
probability distribution is defined as the square root of
the
variance
,
| (1) | |||
| (2) |
where
| (3) |
The square root of the sample variance of a set of N values is the sample standard deviation
| (4) |
The sample standard deviation distribution is a slightly complicated, though well-studied and well-understood, function.
However, consistent with widespread inconsistent and ambiguous terminology, the square root of the bias-corrected variance is sometimes also known as the standard deviation,
| (5) |
Given only a sample of values x1,...,xn from some larger population, many authors define the sample standard deviation by
A slightly faster way to compute the same number is given by the formula
The reason for this definition is that s2 is an unbiased estimator for the variance σ2 of the underlying population. (The derivation of this equation assumes only that the samples are uncorrelated and makes no assumption as to their distribution.) Note however that s itself is not an unbiased estimator for the standard deviation σ; it tends to underestimate the population standard deviation. Although an unbiased estimator for "s" is known, the formula is overly complicated and amounts to a minor correction. Moreover, unbiasedness, in this sense of the word, is not always desirable; see bias (statistics). Some have even argued that the difference between n and n − 1 in the denominator is overly complex and trivial and thus exclude it. Without that term, what is left is the simpler expression
George Huxtable wrote:
Alex wrote-I measure some distance several times, say 7 times in 10 minutes. A star-to star distance can be considered constant for this period. The average is the arithmetic average. (x_1+x_2+x_3+x_4+x_5+x_6+x_7)/7 in this case. Here x_1...x_7 are my sextant readings. The standard deviation. I subtract the average from each x_j, square the difference add the results, divide by 6 and extract the square root. (Actually the calculator does it all for me).==================== One thing puzzles me. Why, in finding the mean of 7 squared-deviations from the average, does Alex (or his calculator) sum them and then divide by 6 rather than by 7? George. ================================================================ contact George Huxtable by email at george@huxtable.u-net.com, by phone at 01865 820222 (from outside UK, +44 1865 820222), or by mail at 1 Sandy Lane, Southmoor, Abingdon, Oxon OX13 5HX, UK. ================================================================