NavList:
A Community Devoted to the Preservation and Practice of Celestial Navigation and Other Methods of Traditional Wayfinding
From: Frank Reed
Date: 2022 May 13, 10:39 -0700
Lars, thanks for the explanation of that geometric method of analyzing lunars. I'm happy to know my "guess" was right. Now that we know what it does, we can consider whether it would have been useful historically or maybe even useful, or at least entertaining, today.
I think we have to throw away the 53/62 advice in the instructions. Maybe that was just a misunderstanding or something unique to the table of chords in "Hints". Clearly we could calculate from this method the primary part of a lunar distance correction. But to what level of accuracy? The factor produced by the geometry gets multiplied by the Moon's HP which must be provided to tenths of a minute of arc (or better, for a little rounding safety). Since the HP has three significant figures, with a maximum around 61.5, we need this factor from the drawn geometry to a precision of three significant figures or maybe a little less. Let's call that one part in 500. For example, suppose the HP is near its average value of 57.5. We need to be sure that the multiplying factor is, say, 0.742 and not 0.744 to guarantee that the resulting parallax contribution to the lunar arc would be, in this case, 42.7' and not 42.8'. So is that possible with normal drafting tools? If our diagram is 20cm across (that's a reasonable sheet of paper), it seems we would need to draw everything and then read it to the nearest half a millimeter (actually 0.4mm). That's possible on a good day, and it might be fun.
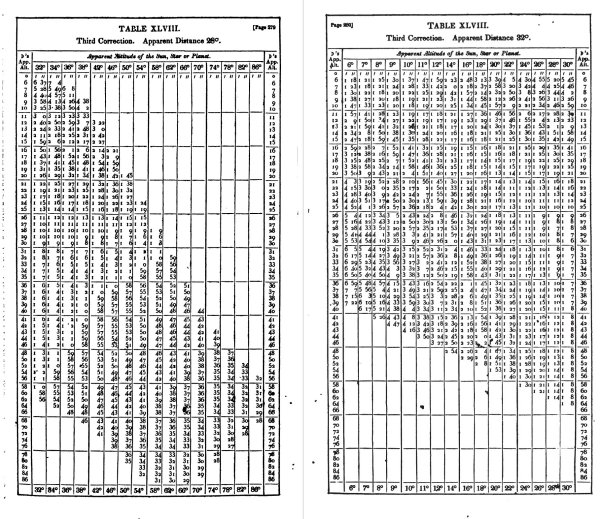
What then do we do about the fact that the method as given completely omits the third correction? ... Of course we can just carry that table. Thomson's table was adopted/stolen as Bowditch's Table 48 in 1837. I'm attaching it below. This makes the whole method a lot less portable and easy, which was the selling point in "Hints", but it would also make it a legitimate method of clearing lunars. The real problem is that the geometric solution does not solve a difficult problem. Working out the parallax contribution to the lunar arc directly from
P = P1 - P2 = HP·sin(ALTm)/tan(LD) - HP·sin(ALTs)/sin(LD) ; (see last paragraph)
by common logarithms to three significant figures is not that difficult. In the modern world we can do this in less than a minute on a calculator. And notice that three significant figures is also within the range of better slide rules (got that slide rule fans??). With extremely careful work, we can get it from the geometric method in "Hints". With any of these computing tools, we can get the major portion of the correction to the lunar distance. The table from Thomson (Bowditch T.48) includes the refraction from both bodies and the two quadratic corrections.
A table like Thomson's, by the way, can easily be regenerated in the modern world, as in the tables in my lunars workshop (just ended). As the Baron von Zach mistakenly believed about Thomson's original table, we can generate these numbers simply by doing the direct triangle solution for all tabulated cases (based on the constancy of the azimuth separation of the Sun and Moon from the observed triangle to the cleared triangle) and then subtract off the quantity P for each case. The remainder is just a few minutes of arc and includes "everything" except the principal correction from the Moon's parallax. In practical use, we turn this around and calculate that principal correction from logs or on a calculator and then look up the "third correction" in the table. Easy and accurate.
It should be said that Thomson didn't invent this methodology. It had been in use for at least two decades before him and was re-discovered multiple times. Thomson's tables had the advantage of including a page for every lunar arc in 4° increments which implied that no interpolation was necessary. Earlier tables, not so finely divided, did not require much more than eyeball interpolation, but no interpolation is clearly better than a little interpolation. There was a German analysis of the history of all of this which mistakenly credited a navigator-mathematician named Elford from Charleston, South Carolina (I wonder if he lived near Longitude Lane! :) ) with the invention of this system. Although Elford had published an early version of tables like this, they were crude compared to later publications. Poor Elford had the misfortune of writing to the Baron de Zach (same baron from above... sometimes he was "von", sometimes he was "de Zach") and complaining bitterly that people were stealing and publishing his (Elford's) correction table. Since Zach published his own well-read "scientific journal" (more equivalent to a "blog" in the 21st century), he did what he thought was right and published Elford's table in his journal making it available for all to copy!
A final note: This "P", above, was not a "new thing". If you've ever read my "Easy Lunars" essay from 2004 (written a few months before the NavList banner photograph that we discussed recently) you've heard me refer to the cosines of the angles at the Moon and Sun corners of the ZMS (Zenith-Moon-Sun) triangle as the "corner cosines". They tell us what fraction of the altitude correction is projected onto the lunar arc. Call them A and B. In the standard series solutions for lunars as described in that essay (which historically go back to Lacaille and Lyons and others in the late 18th century), we get the cleared lunar distance from
LDc = LDpc + dhm · A + dhs · B + Q,
where LDpc is the "pre-cleared" lunar distance (semi-diameters dealt with), dhm and dhs are the ordinary altitude corrections and Q is the total "quadratic correction", variously calculated and tabulated in early methods of clearing lunars. The only trick in Thomson-style tables is to split the Moon's altitude correction. The Moon's refraction correction plus the star's altitude correction and Q all go into that big table, but we still calculate [HP·cos(Altm)]·A. Since there's another cos(Altm) in the denominator of A, they cancel out and we end up with the relatively simple and short computation of P as given above. To sum up, P is the Moon's parallax in altitude multiplied by the corner cosine at the Moon. All the other little bits are in that big table.
Frank Reed