NavList:

Hi Andrew

About a week ago, you proposed a question. To sumarize, you requested the height of the apex of a string above the surface of the earth, when that string is 1" longer than the circumference of the earth. The string is pulled from one point upwards.

Only two responses have been posted, one by Frank and one by myself. Frank obtained 180 feet (2160") for the height of the apex and I derived 413.32". These values are in obvious disagreement. Since you posed the question, I can only assume that you know the correct answer!!

As an engineer, I must first verify my assumptions and construction of the problem. I may have done something wrong. In fact, it happens all the time. So rather than question Frank's numbers, I question my own.

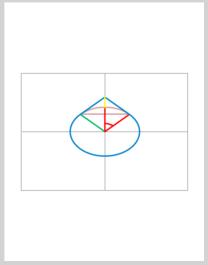
Please examine Figure 1 - 45 degrees. In this image we can see my construction of the problem. I create an angle of 45 degrees, shown in red. This angle is mirrored about the vertical axis, in green. Where the line constructed by the angle touches the circumference of the earth, we have a tangent line to the circle, in blue, that intersects with the vertical axis. This tangent line is mirrored about the vertical axis, also in blue. Finally, we have the arc around the earth where the string is touching, also in blue. When we sum the lengths of the three blue lines (tangent line segment 1, tangent line segment 2 and arc length), we have the length of the string.

Also in figure 1, you will find a yellow line. This is your requested height of the apex of the string above the earth. We find this length by subtracting the radius of the earth from the Y-intercept of the tangent line.

Now that the description of the figure is complete, we can readily verify the construction, particularly as the angle is 45 degrees.
1) The length of the first tangent line segment should be precisely the radius of the earth, 251103108.1953 inches. It is!
2) Since we have a 45-45-90 triangle, the Y-intercept should be sqrt(2*radius^2)=355113421.1639 inches. It is.
3) The circumference of the earth is 1577727360 inches. 3/4 of that (360 deg-45deg-45deg) is 1183295520 inches. Is our arc length equal to that? It is.
4) Is the sum of the lengths of the two tangent line segments plus the arc length equal to 1577727361 inches? NO! it is 1685501736.3907 inches, a tad long to satisfy the problem statement.
5) The resultant height of the apex is 104010312.97 inches.

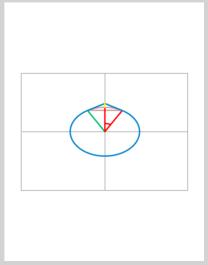
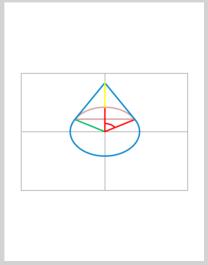
I include Figure 2 - 30 Degrees and Figure 3 - 60 Degrees such that the informed observer can see how the construction varies with the angle.

For 30 degrees, we have
1) Arc length = 1314772800.000 inches, which is 5/6 of the circumference of the earth. Correct.
2) Tangent line segment length 144974447.1109 inches.
3) Sum of segments = 1604721694.2219 inches. NOT equal to the problem statement.
4) Height of Apex above the earth's surface is 38845786.03 inches.

Similarly, for 60 degrees, we have
1) Arc length = 1051818240.0000 inches, which is 2/3 of the circumference of the earth. Correct.
2) Tangent line segment = 434923341.3328 inches.
3) Sum of segments = 1921664922.6655 inches. NOT equal to the provlem statement.
4) Height of Apex above earths surface = 251103108.20 inches.

How about when the angle is zero? No figure needed.
1) Arc length = 1577727360 inches, the circumference of the earth. Correct.
2) Tangent line segment = 0 inches. Correct.
3) Sum of segments shy by 1 inch. Correct.
4) Height of Apex =0. Correct.

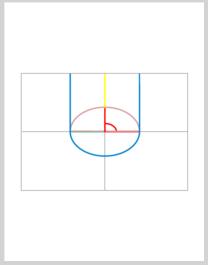
How about when the angle is 90 degrees? In figure 4, I show when the angle is actually 89.999999999999 (twelve nines). This permits us to check to see that the arc length is very close to 1/2 of the circumference. The value obtained for the arc length is 788863680.0000 inches. Correct again! The tangent line segments are huge values. Now this is a very interesting construction that I will begin a new topic for.

How about when the angle is 0.103957188 degrees?
1) The arc length is 1576816159.4457 inches.
2) The Tangent line segments are 455600.7771 inches.
3) The sum of segments is 1577727360.9999 inches. To within one part in 10000 of an inch to the correct value of 1577727361.0000 inches.
4) The Y-Intercept is 251103521.52 inches and therefore, the height of the apex is 413.32 inches.

I believe that my construction is correct. I cannot find fault with it.

Would you kindly post your answer to your question Andrew, under the assumption that you know it?

Best Regards
Brad

----------------------------------------------------------------
NavList message boards and member settings: www.fer3.com/NavList
Members may optionally receive posts by email.
To cancel email delivery, send a message to NoMail[at]fer3.com
----------------------------------------------------------------

File:

  

File:

  

File:

  

File: