NavList:

   

Reply

First the easy answer: yes, the graph is for geodetic latitude.

Now the more nasty one: why is there a 1/60th difference in size of a 
minute at the poles vs at the equator (actually it is a bit less, about 1%)?
In order to calculate the length of 1 arc minute in latitude on the 
ellipsoid for a given latitude we can use the following deceptively easy 
formula:
m = rho * sin (1/60) where
    m = length of one arc minute in metres
    1/60 = one arc minute (1/60th of a degree)
    rho = curvature of the meridian for the given latitude

Rho can be calculated from a slightly more complex formula:
rho = a*(1-e^2)/SQR((1-e^2*SIN(lat)^2)^3) where
    a = the Earth' semi-major axis (6378137.000m for WGS84)
    e = first eccentricity
    lat = the required latitude

Finally e can be calculated from another simple formula:
e^2 = (a^2 - b^2)/(a^2) where
    a = semi major axis (6378137.000m for WGS84)
    b = semi minor axis (6356752.314m for WGS84)

or from:
e^2 = (1/Finv)*2-(1/Finv)^2 where
    Finv = inverse flattening (298.257223563 for WGS84) which can be 
calculated from:
    Finv = (a-b)/a

We can now calculate the curvature for every latitude we wish:
0 degrees: 6335439.327m
30 degrees: 6351377.104m
60 degrees: 6383453.857m
90 degrees: 6399593.626m

Now we see that the curvature is something else than the length of the 
axis of the ellipsoid and this has all to do with the shape of that 
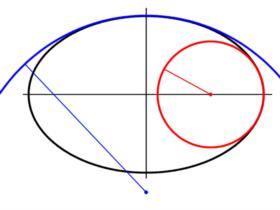
ellipsoid. Attached you will find a small drawing of an ellipse 
(basically a slice of earth). The black ellipse is where we live on in 
slightly exaggerated proportions. It has a major (drawn horizontal) and 
minor axis (drawn vertical). I tried to make a best fit for the 
curvature near the equator (red) and near the north pole (blue). The red 
and blue dots are the centres of these two circles. As you can see the 
radius of the red circle is only half the semi major axis, while the 
blue circle 1.5 times the semi major axis. So the circles have a 1:3 
ratio (making 1 arc minute near the pole three times as large as one arc 
minute near the equator), while I have drawn the ellipse at a 1.5:1 
ratio, which leads to the conclusion that the ratio's have a 1:4.5 ratio 
(is this getting confusing?).

Nicolàs


Lu Abel wrote:
> Curiosity question:
>
> It's well known that the diameter of the earth across the equator is 
> about 1/300th greater than the diameter across the poles.
>
> I would intuitively expect, therefore, that the size of a minute of 
> latitude to change by a like amount.  But looking at this graph, there 
> seems to be a 1/60 difference in the size of a minute at the poles vs 
> at the equator.  Is there an explanation that this technically 
> competent, but ignorant of the math of the oblate spheroid, person 
> could understand?
>
> Also, I assume this graph is for geodetic latitude and not geocentric 
> or parametric latitude?
> (For people curious about these terms, geodetic latitude is what you 
> get by drawing a line perpendicular to the surface of the earth down 
> to its axis.  Due to the flattening of the earth, this line will 
> intersect the earth's axis on the other side of the equator from the 
> observer's position.  The other two latitudes are what you get when 
> you draw a line out from the earth's center. This line is not 
> perpendicular to the earth's surface except that the poles and equator)
>
> Lu Abel
>
> Nicolàs de Hilster wrote:
>> On NavList 7052 Irv Haworth wrote:
>>   
>>> "I think it's well known that 1' of arc varies in length as a function
>>> (cos)
>>> of the latitude."
>>>
>>>   
>>>     
>> On which Gary LaPook replied in NavList 7053:
>>   
>>> That is true for one minute of longitude because parallels of latitude are small circles.
>>> This is not true for one minute latitude of for any 
>>> other great circle. (Technically these also vary slightly due to the 
>>> oblateness of the earth but these small variations are ignored for
>>>  celestial navigation purposes.)
>>>   
>>>     
>> For those who want to know how much exactly that variation is I posted 
>> attached graph of it in NavList 4750 on 24/03/2008.
>>
>>
>> >>
>>   
>>
>> ------------------------------------------------------------------------
>>
> ------------------------------------------------------------------------
>
>
> No virus found in this incoming message.
> Checked by AVG - http://www.avg.com 
> Version: 8.0.176 / Virus Database: 270.10.7/1894 - Release Date: 1/14/2009 7:27 PM
>
>   


--~--~---------~--~----~------------~-------~--~----~
Navigation List archive: www.fer3.com/arc
To post, email NavList@fer3.com
To , email NavList-@fer3.com
-~----------~----~----~----~------~----~------~--~---

File:

   

Reply