NavList:

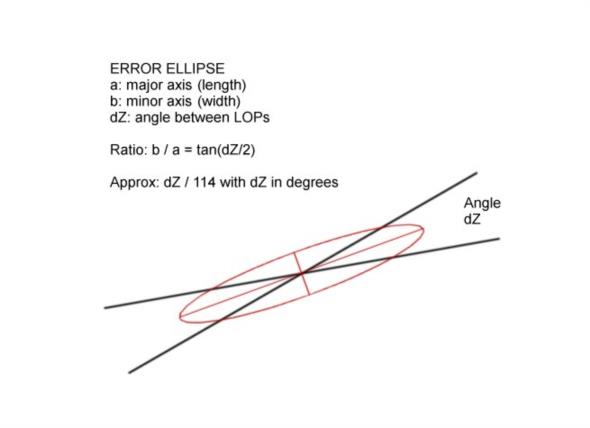
You shoot two stars separated in azimuth by some degrees. The resulting LOPs cross at an angle between 0° and 90°. Let's call that angle dZ. The lines cross at a point, and that is your fix. Around that, you would like to draw in a rough error ellipse. Its size is determined by your estimate of the error in your sights and also by the confidence level you're looking for. The long axis of the ellipse will run along the line splitting the difference between the two LOPs. But what determines its shape? That is, what is the proportionate length of the long axis of the ellipse compared to the short axis, or, if you like, the "aspect ratio" of the error ellipse? Turns out there's a relatively simple formula for it, which can be derived from the usual rules for a statistical fix (details in PS). It is
  b/a = tan(dZ/2).
There is a very nice fast approximation for this: the ratio is dZ/114 when dZ is in degrees. So if you have two sights separated in azimuth by about one compass point (11.25°), the ratio of the length of the ellipse to the width is just about 10-to-1. If the sights are separated by two compass points then the ratio is about 5-to-1. And so on. See attached image.

Frank Reed
Clockwork Mapping / ReedNavigation.com
Conanicut Island USA

PS: (this version from my recent "Advanced Modern Celestial" class; original in Nautical Almanac)
STATISTICAL FIX

• Get intercepts, a_i and azimuths, Z_i for multiple sights (advanced for run, if necessary).
• A = Σ [cos(Z_i)]².
• B = Σ cos(Z_i) × sin(Z_i).
• C = Σ [sin(Z_i)]².
• D = Σ a_i × cos(Z_i).
• E = Σ a_i × sin(Z_i).
• F = Σ [a_i]².
• G = A×C - B².
• Lat = APlat + (C×D - B×E) / G.
• Lon = APlon + (A×E - B×D) / G / cos(APlat).

ERROR ELLIPSE

• Ellipse, centered on fix, has major axis, a, with minor axis, b, perpendicular.
• Standard deviation, σ (sigma), of observations may be estimated as an input or calculated from observations.
• Multiply σ by 1.2 for 1 s.d. ellipse or 2.4 for 2 s.d. ellipse ("95% ellipse").
• X = 2B / (A - C)
• DZ = [tan^-1(X)].
• a = σ / √[N/2 + B/sin(DZ)]; N is total number of sights.
• b = σ / √[N/2 - B/sin(DZ)].
• Ellipse is oriented along azimuth Z, given by DZ / 2.

File: