NavList:
A Community Devoted to the Preservation and Practice of Celestial Navigation and Other Methods of Traditional Wayfinding
From: Frank Reed
Date: 2013 Apr 2, 10:36 -0700
I wrote previously:
"Speaking of treating dip as an unknown, for any of you who were following the thread about measuring dip, you can measure it with an ordinary properly adjusted sextant as long as your goal is just collection of data for statistical analysis (as opposed to live navigation). You measure altitudes from a known location and clear them treating dip as unknown (set to zero). Then the error in the sights is equal to your dip."
And Brad Morris, you commented:
"That's under the assumption that ALL other errors are zero. That's a mighty big zero to shoot for. Any error will be treated as an estimate of dip."
Yes, in that little phrase of mine "properly adjusted sextant", there's a lot of detail that I skipped for the sake of brevity. But let's put it this way, if you have a decent quality metal sextant that you have used to shoot lunars or accurate horizontal terrestrial angles, for example, and you have found that the approximate standard deviation of individual observations is one-quarter of a minute of arc, then that's good enough for measuring any significant variability in dip (since, as you've already noticed, there are very short-term variations in the horizon that are about that size and therefore there's no meaningful definition of the horizon at better than 0.1 to 0.2 minutes of arc resolution). If you can measure lunars or terrestrial horizontal angles to an accuracy of a couple of tenths of a minute of arc, but you find that your altitude observations have a variability of three or four times that, then the only source for this additional variability is some flaw in the observation process (not likely from land, as long as the observer knows how to swing the arc properly and record time properly) or the horizon itself.
Let's be very clear on this: the SINGLE BIGGEST UNCERTAINTY in standard line of position celestial navigation (or any celestial navigation that is equivalent to LOP celestial) is the uncertainty of the horizon --the variability of dip. I've been saying this for years in classes, though I'm not sure how often I say it in NavList messages. And there is nothing that can be done about this. It can be interesting (and "fun" as you said a while back) to observe this variability to get some real sense of how large the effect is. But "solving" this problem is a wild goose chase. And it's a goose that the developers of navigational methods have been chasing for over 200 years! Refraction near the horizon depends on the complex structure of density variations in the air. Some model cases, like a linear decrease or increase of air temperature as a function of height (known as the "lapse rate") can be calculated and used to get a general sense of the scale of possible variability. But these model cases are too simple to be used to explain specific practical cases of observation, especially near the shore, which is exactly where you're making your observations.
And again, these sorts of observations, like using a theodolite (which is certainly easier IF you have one available) or using a properly adjusted sextant from a known location are one "class" of dip observations where the purpose is to collect data, not to contribute directly to live navigation. The Soviet-era dip meter which Alex Eremenko kindly showed us and has allowed you to borrow is a different animal. The underlying assumption for that device is that dip is sometimes not predictable in any reasonable way, for example in Arctic waters, and a better option is to treat it as an unknown in such special circumstances and measure it for "live navigation" synchronized with a series of sextant observations. Then the dip is simply a feature of the observation with no theoretical modelling required at all. You could also do this at sea with two high altitude sights. Consider the Sun at noon from Montauk in late June. You shoot a normal altitude of about 72 degrees. Then you turn around and shoot a backsight of about 108 degree, which is well within the range of a standard sextant. If there's no arc error and if the telescope is properly collimated (relatively important for such large angles), then the sum of the two altitudes will be 180+2*dip.
There's yet another way to correct for anomalous dip in live navigation which is closely related to the "cocked hat" discussions that were so fatiguing last month, and it's essentially the method that was taught to USN navigators in the 1950s and 1960s which Byron Franklin refined and implemented.
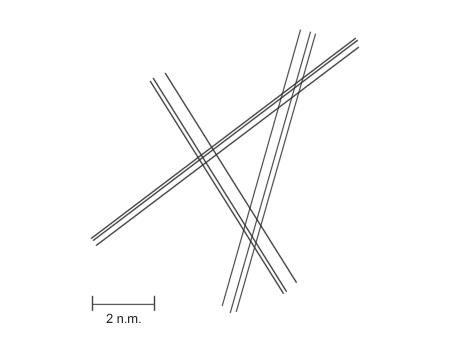
A couple of folks in the earlier "cocked hat" discussion commented that they would prefer to shoot several sights in a row of two bodies rather than shooting one sight each of three or more bodies. But anomalous dip is a type of constant "systematic error" which would not be detected if only two bodies are used. Imagine shooting three sights each of three stars. If the resulting LOPs of each sight for each star show little difference, within some relatively small scale of difference, like for example 0.3 minutes of arc, while the resulting plot has an open central area ("cocked hat" since there are three bodies) that is noticeably large, say for example 1.5 minutes of arc, then we have excellent evidence of systematic error. See the attached diagram. And notice that this would be completely undetectable if only two bodies were used. This clearly identifiable systematic error can be eliminated by adding or subtracting some offset from all of the sights until the new LOPs make a small "spider web" with the overlap area as small as possible (and this can be done directly on the plot --there's little actual work required). This technique does, however, make the assumption that the systematic error is CONSTANT, which may not be true. There's no reason to identify the cause of this systematic error in normal navigation, but unless there is reason to believe that the index correction was wrong, the most likely origin is anomalous dip. Notice that various other types of sextant errors, like arc error, would yield a variable systematic error, and in that case eliminating a constant systematic error would give misleading results. Also, there could always be some systematic error that applies to only one body -- something as simple as recording the wrong minutes of arc from the almanac data in one star's declination (e.g. 54.2' instead of 52.4'). An error like that could create the illusion of a constant systematic error when in reality it's an error in a single group of sights. So there's some "detective work" involved, but nothing too difficult.
Finally, it is critical to note that this systematic error cannot be detected if only one sight each of three bodies are available. It was a common misconception a few decades ago that the procedure for cancelling systematic error was a procedure for cancelling all error. Some navigators routinely added or subtracted an offset from each site to get the true "fix" instead of using the so-called "symmedian point" which is the most probable position based on an assumption of random error, a.k.a. "noise" in the observations, rather than systematic error. This is a long-lasting error which entered into common practice among many skilled and experienced navigators, but an error it is.
-FER
----------------------------------------------------------------
NavList message boards and member settings: www.fer3.com/NavList
Members may optionally receive posts by email.
To cancel email delivery, send a message to NoMail[at]fer3.com
----------------------------------------------------------------