NavList:

Note:when lookin for some old paper I found this to Naval proceeding. Itink that it was some interest to the small boat and other seaman. The compass check accuracy is one of the benifits. I don't know if it was published? About 1985?
Richard Kabrick
Surface Warfare Officers
Division Officers Course
Bldg 370, NETC
Newport R.I. 02840
(401) 841-3055 correct Gyro. I don’t know if
Editor Proceedings used it? The date
Proceedings Date around 1985?.
US Naval Institute
Annapolis, MD. 21402
The following is submitted for consideration for a future edition of “Proceedings” in the professional section.
DETERMINING GYRO ERROR PIERSIDE (DISTANT OBJECT METHOD)
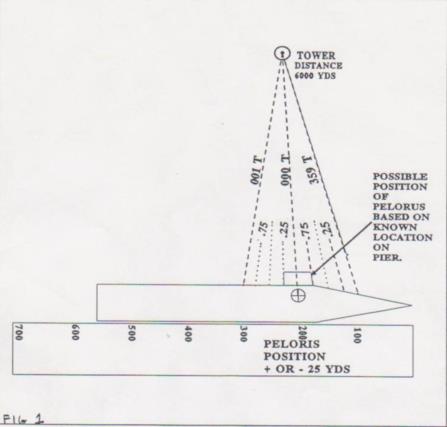
There are two generally accepted and practiced methods of determining gyro error while the ship is still moored to the pier. Each method has validity as well as certain inherent problems. The first is by celestial observation using the Sun or Polaris. An Azimuth of the Sun is accomplished by obtaining a bearing to the body, noting the time and observers position, and utilizing the reduction tables or suitable calculator/computer programs a comparison is made to what the body should bear, any difference is then Gyro error. In addition to a rather lengthy calculation process these methods have an accuracy that is questionable beyond one half of a degree. Additionally these procedures are usually done a significant time prior to the ship getting underway, this can leave doubt as to whether there has been any changes to the original determination. The second method is the pierside fix or trial and error method. Here a fix is taken by utilizing three or more LOPs, if this results in a pinpoint fix then gyro error is assumed to be zero. If however, a triangle results, equal amounts of an assumed error are applied to each LOP until a pinpoint fix is achieved. This method again is time consuming and if the objects used for the fix are a relatively short distance away an error may not be apparent even though one exists. An easy and accurate method does exist which utilizes the Rule of Sixty (Radian Rule). Since a Radian measures just under 60 degrees we can assume that it represents one-sixth of a circle. If we know the distance to an object, then we know that we are on a circle which has a radius of that distance from that object. Next by dividing that distance (radius) by sixty we can identify what each degree of bearing along that portion of the circle is worth in terms of distance. This can be used for many purposes. One use is a quick and accurate way to determine gyro error. All that is required is to estimate your position alongside the pier, determine how accurate your position is known + or - 10, 15, 20 yds etc. Once this value is known double it and multiply by 60 ‘ result is the minimum distance you want an object to be in which to obtain a bearing to. In our example we ye determined our position on the pier to be within 25 yards, doubling that amount we get 50 and multiplying 0 we get 3000. Any object we use must be at least 3000 yards away to obtain the accuracy we need. In fig 1.
the tower is 6000 yards away so it meets our criteria. Looking at the chart the towers bearing should be 000 degrees true. Knowing that it would take 100 yards (6000 yds divided by 60) of movement at right angles to the tower to change its bearing by one degree any difference in an observed bearing will be gyro error known to within one fourth of a degree. The shaded area in fig 1 represents the possible location of the pelorus since the position was estimated to be within 25 yards (one fourth of 100). Assume that our observed bearing was 359 degrees per gyro compass. The true bearing from the chart should have been 000 therefore a one degree east error (gyro least error east) is present that is known to be accurate to within one fourth of one degree because the true bearing to the tower could be from 359.75 to 000.25 degrees. This explains why the pierside fix can be misleading, assume all LOPs used were at a distance of less than 2000 yards, if an error of one degree was present the resulting LOPs would have a visible error on the chart of less than 35 yards (2000 divided by 60). This would not cause much alarm on most harbor charts, however once off the pier where more distant objects are used this error (still unidentified) results in triangles and low confidence fixes. Another use is shown in fig 2. Here an anchored vessel is observed ahead of our track, a channel buoy and a point of land are also observed, all of which are at an approximate distance of 2000 yards (obtained from radar). We desire to know how much distance is between the ship and the buoy and the ship and point of land (Distance between objects)(DBO). From the pelorus we observe an angular separation of 10 degrees. Therefore we can quickly compute that there is approx 333 yards DBO. (2000 divided by 60 = 33, 33 times 10 = 333. Between the ship and the land we note there is 15 degrees of separation so we can quickly determine 500 yards DBO (2000 divided by 60 = 33, 33 times 15 500). This technique can be of great assistance to Commanding Officers, Navigators, OODs and other bridge personnel.
References:
1. “The Franklin piloting technique” American Practical Navigator Vol 1, 1984 ed. Art 1008.
Picture 1.
----------------------------------------------------------------
NavList message boards and member settings: www.fer3.com/NavList
Members may optionally receive posts by email.
To cancel email delivery, send a message to NoMail[at]fer3.com
----------------------------------------------------------------