NavList:
A Community Devoted to the Preservation and Practice of Celestial Navigation and Other Methods of Traditional Wayfinding
From: Frank Reed
Date: 2020 Jan 14, 11:37 -0800
Rafael, you wrote:
"The answer to Frank’s last message deserves paraphrasing Dr. Watson’s memorable remark “You amaze me, Holmes! I mean, Reed!” The sextant sights I posted were indeed taken around local noon on Saturday, November 16, 2019, which was a sunny, cool, and windy day on the Jersey shore. After recovering form my surprise, I reasoned that if one can calculate a position given date, time, and altitude, one might also be able calculate a date given position, time, and altitude. Still, it was very elegantly done!"
Ha ha. But right? I was entertained that I could pin it down to the day, too. The noon altitude is almost enough information, but you didn't say whether the altitudes as graphed were corrected or uncorrected (it's clear from the final result that you had plotted the corrected altitudes), and it was always possible that you had done your plotting with some offset, or the sights might have even have been from early last year. But it turned out that the time (UT) of noon was a relatively good test of position, too. This is unique to the season. Between November 4 (Sun Fast Day) and February 11 (Sun Slow Day), the Equation of Time changes by half an hour. That corresponds to 7.5° of longitude --the width of half a timezone. So if you know the UT of noon (which we were able to determine from your graph, from folding or from your quadratic fit), that could shift your position from somewhere out in the Atlantic to somewhere in western Pennsylvania, depending on the date. It was this high sensitivity to longitude during this part of the year that gave an independent verification of the date.
You added:
"Curve fitting was impractical before the computer age, but the tracing paper method, which relies on visual alignment, was definitely available."
And yet it was almost unknown. Folding the graph is something that I have been promoting and teaching in classes for the past ten years. Before then, longitude by sights around noon had been shunned for decades (with few exceptions). There were two key problems with earlier graphical methods for getting the axis of symmetry of a noon curve: 1) navigators were encouraged to "fair in a curve" which is a very bad idea. The hand of the artist is inevitably drawn to certain points on subjective grounds, and 2) for real navigation, aboard vessels which are in motion, the time of the axis of symmetry must be adjusted, and this correction was largely unknown or ignored.
Hewitt Schlereth mentioned his nice little book on this topic from the 1980s. It includes tables for that motion correction which made it a major improvement on earlier accounts, but it didn't quite get the attention of the stodgier corners of the world of navigation. It's not hard to see why there has to be a correction for motion. Suppose you're sailing due south at 6 knots. Suppose also that the Sun at high noon is south of you, and you plan to take a dozen sights over the course of 40 minutes centered around local noon. At that speed your latitude is decreasing at a rate of 1' every ten minutes of time. So that means that the last sight that you take at the end of your 40-minute run will be higher than it "should be" by 4 minutes of arc. Each of your dozen sights during those 40 minutes will be nudged up in proportion to the time. If you plot that out, you'll see that the axis of symmetry is then shifted toward the right on the graph (the peak occurs later). In terms of geometry, we are adding a sloping straight line onto a (near) parabola. The result is a different parabola, possibly shifted up or down a little and significantly shifted to left or right.
You might think standing on a boardwalk in New Jersey that you're free from any worries about motion. There's no vessel motion, but the Sun's declination is always changing during the day. On November 16, the Sun was still heading south at a rate of 0.6 knots (Dec decreasing 0.6' per hour). The effect is identical to vessel motion. Over a 40-minute run of sights, the Sun would be lower at the end by 0.4' than it would have been without the changing Dec. Now that's not much and you could ignore it. That's a viable option. Another good option for this scenario, assuming a long enough boardwalk (!), is to chase the Sun. If you had walked south at a normal walking pace for a minute or two between each pair of sight, you could have cancelled out the Sun's motion away from you. But in the general case, we can just figure out the relative speed between observer and vessel. For example, next March if I'm doing this at local noon in a boat sailing south at 5 knots, I know that the Sun is coming north at 1 knot at that time of year, so I am approaching the Sun at a net speed of 6 knots.
So what's the correction for relative motion? Some straight-forward algebra and trig around noon will demonstrate that the correction, dt, in seconds of time is
dt = 1.53 · v · (tan Lat - tan Dec).
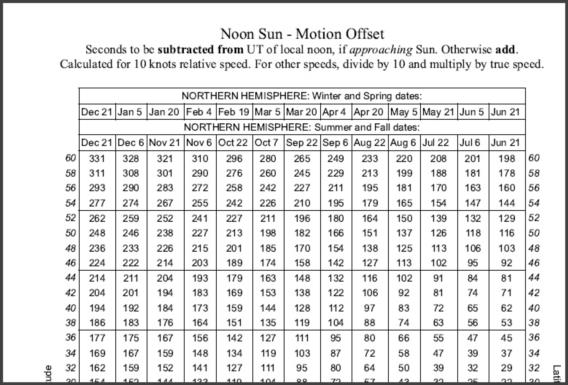
where Lat is best estimate of latitude, Dec is the Sun's declination at noon, and v is the relative N/S speed in knots between the subSun point and the vessel, as in the example above. Now that correction is pretty simple to work up on a modern calculator, but we can also tabulate this. And since the Sun's Dec is constrained by calendar date, we can build a table that's entered by date. Attached below is an example of such a table that I provide in my classes.
Finally, let's get back to your original question. Is the curve a parabola? No... It's very close. But suppose you want to do a modern analysis of this that's "honest" and fits to a curve with the proper shape. This is not hard in a spreadsheet. Enter your sight UTs and decimalized altitudes in two columns. Then directly calculate the altitude of the Sun at each UT in another column from the fundamental spherical triangle formula:
sin(Alt) = sin(Lat)·sin(Dec) + cos(Lat)·cos(Dec)·cos(GHA-Lon).
Dec is known for the time of the sights. GHA is simply proportional to time from the midnight value of GHA. Lat and Lon can be free parameters (in cells in the top row of the spreadsheet maybe). Then in another column, calculate the simple difference between the (corrected) observed altitudes and these computed altitudes. Then calculate the sum of the squares of all those differences (you can use a spreadsheet's built-in VAR() or STDEV() functions as equivalents). Now vary Lat and Lon until the sum of the squares is minimized. That's your position. Note that this is just how the process of quadratic curve fitting works (it minimizes the sum of the squared differences to the curve), but with this analysis you're using the curve with the proper shape.
Frank Reed
Clockwork Mapping / ReedNavigation.com
Conanicut Island USA