NavList:

   

Reply

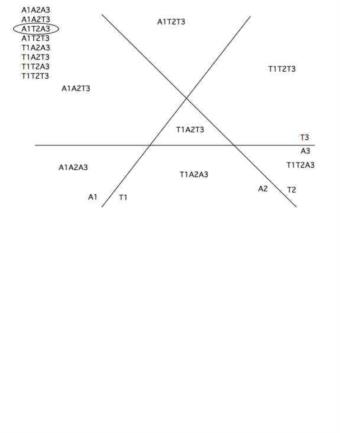
On Mar 15, 2007, at 11:24 AM, George Huxtable wrote:
> Fred contributed- "A small triangle suggests that sigma is small for
> each line, and a large
> triangle that sigma is large". I agree that a large triangle implies
> that there's a lot of scatter, but the contrary isn't true of a small
> triangle; it depends a bit on what Fred means by "suggests".
>
> Indeed, a single cocked-hat gives little clue to the possible scatter
> in the true position. Just by chance, it might well happen to be a
> tiny triangle, but that doesn't allow a navigator to deduce that the
> resulting position is a precise one. It's only after assessing the
> sizes of a large number of such cocked hats that a navigator could
> come to such a conclusion. Not a practical proposition really; in its
> place he has to fall back on common sense and experience, in
> estimating what his observation errors are likely to amount to.

Yes, this was a statistical argument, perhaps with more precision, it
might be phrased as, 'the cocked hat will tend to get larger as sigma
increases.'  So yes, one could get a small triangle with a large
sigma; one would need to assess a series of fixes, and be aware of
error factors such as bad horizon, anomalous dip, tired navigator,
cocky navigator, etc.

With no error (sigma = 0), there will be no cocked hat: three
position lines will intersect at one point.  The _average_ area of
the cocked hat will increase with error.  That is another fairly
precise phrasing of the same thought.

> Separating those two scenarios, of azimuths that embrace more than 180
> degrees and those that embrace less, is the dividing case of azimuths
> that are just 180 degrees apart. As Fred points out, in that case the
> triangle degenerates to a straight line. It isn't a triangle at all,
> and there's little point in considering that special case in any
> detail, though I'm a bit puzzled how Fred manages to make 7
> possibilities out of it.

Just considering the plane geometry, three lines that do not
intersect at one point and are not parallel to each other divide the
plane into seven areas, not eight.  Here follows a diagram of this.
In this example, the eight possible combinations of toward and away
are listed.  The circled combination, A1T2A3, does not seem to be
possible in this configuration.  And there is only one position
inside the triangle, T1A2T3.  I'm not sure what's going on and where
A1T2A3 is hiding.  I believe George discussed this previously.

Fred Hebard



--~--~---------~--~----~------------~-------~--~----~
To post to this group, send email to NavList@fer3.com
To , send email to NavList-@fer3.com
-~----------~----~----~----~------~----~------~--~---

File:

   

Reply