NavList:
A Community Devoted to the Preservation and Practice of Celestial Navigation and Other Methods of Traditional Wayfinding
Re: Celestial up in the air
From: Gary LaPook
Date: 2008 Jul 24, 02:34 -0700
From: Gary LaPook
Date: 2008 Jul 24, 02:34 -0700
A little more information about MOB adjustments. If you use the MOB
tables in H.O. 249 (pages 5 & 7 of PDF) the easiest way to keep
from confusing yourself regarding the sign of the adjustment is to
simply draw a horizontal across the center of the table and put a big
minus sign for the top half and a big plus sign for the bottom half of
he table. This will provide the sign for the usual case of a sight
taken prior to the fix time and the adjustment being made to Hc.
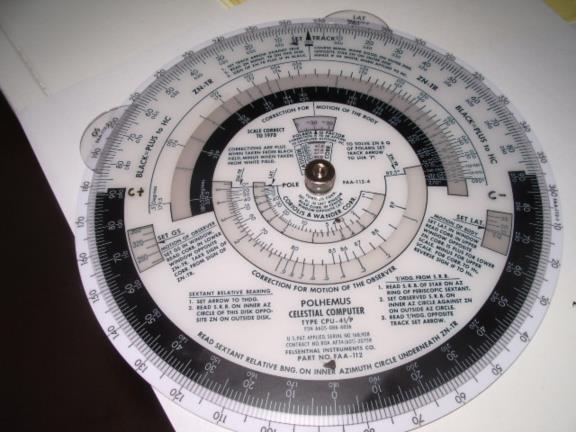
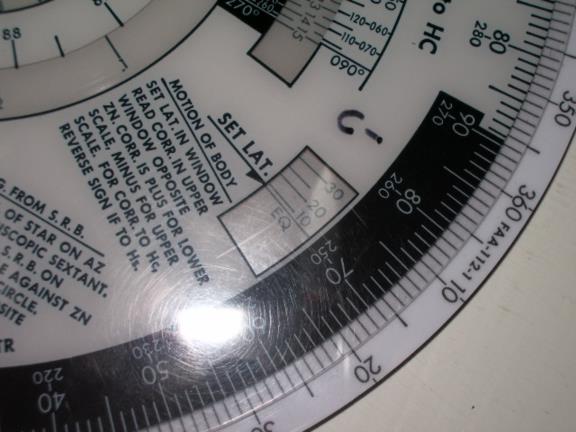
Another way to derive the MOB adjustment is to use the Polhemus computer. At first glance the front of this device looks intimidating (see image 1, attached) but in fact it only requires setting three parameters in the appropriate windows and then reading out the MOB adjustment as well as the "Motion of the Observer" (MOO) and the coriolis correction (more about these later.) Image 2 shows a zero degree latitude set in the latitude window which is all you need to do to find the MOB adjustments. Now by looking at the azimuth scale along side of the MOB window you can take the MOB adjustment from the adjacent scale inside the MOB window, see image 3. Since this is set to 0º latitude you will find that the MOB adjustment is 15' for an azimuth of 90º and 7.5' for an azimuth of 30º just the same as on page 7 of the PDF, the one minute MOB table. Image 4 shows it set for a 60º latitude and you find an adjustment of 7.5' for 90º and 3.8' for an azimuth of 30º just like the table on page 7. If you compare the other values on the Polhemus with those tabulated on page 7 of the PDF you will see that the Polhemus produces identical adjustment factors. In fact, the Polhemus might be able to produce greater accuracy since you can read out the factors for intermediate values instead of mentally interpolating on the MOB table or just simply taking the closest tabulated value.
If you are really concerned with accuracy you can calculate the MOB on your calculator using the formula:
MOB = 15' x cos LAT x sin Zn .
gl
Gary J. LaPook wrote:
--~--~---------~--~----~------------~-------~--~----~
Navigation List archive: www.fer3.com/arc
To post, email NavList@fer3.com
To , email NavList-@fer3.com
-~----------~----~----~----~------~----~------~--~---
Another way to derive the MOB adjustment is to use the Polhemus computer. At first glance the front of this device looks intimidating (see image 1, attached) but in fact it only requires setting three parameters in the appropriate windows and then reading out the MOB adjustment as well as the "Motion of the Observer" (MOO) and the coriolis correction (more about these later.) Image 2 shows a zero degree latitude set in the latitude window which is all you need to do to find the MOB adjustments. Now by looking at the azimuth scale along side of the MOB window you can take the MOB adjustment from the adjacent scale inside the MOB window, see image 3. Since this is set to 0º latitude you will find that the MOB adjustment is 15' for an azimuth of 90º and 7.5' for an azimuth of 30º just the same as on page 7 of the PDF, the one minute MOB table. Image 4 shows it set for a 60º latitude and you find an adjustment of 7.5' for 90º and 3.8' for an azimuth of 30º just like the table on page 7. If you compare the other values on the Polhemus with those tabulated on page 7 of the PDF you will see that the Polhemus produces identical adjustment factors. In fact, the Polhemus might be able to produce greater accuracy since you can read out the factors for intermediate values instead of mentally interpolating on the MOB table or just simply taking the closest tabulated value.
If you are really concerned with accuracy you can calculate the MOB on your calculator using the formula:
MOB = 15' x cos LAT x sin Zn .
gl
Gary J. LaPook wrote:
Before I can give an example of how celnav is done in flight I must explain how some things are done differently in flight.
The first thing to discuss is the "motion of the body" adjustment. The marine practice is to take the sight, consult the almanac for the GHA of the body (or Aries) for the even hour before the sight and then add an increment for the minutes and seconds after the hour. The navigator then chooses an assumed longitude to make the the LHA used in the computation a whole number of degrees.
It is done differently in flight. The flight navigator plans a fix time on the hour or at even ten minute intervals after the hour (the Air Almanac publishes data for every ten minutes) and takes out the GHA without any interpolation. He then chooses an assumed longitude to make a whole number of degrees of LHA and computes his Hc based upon this. Since two out of the three sights will be taken earlier than the fix time it is necessary to make adjustments to allow for this and this is what the "motion of the body" adjustment is all about and this is how it works. Think this one through. Imagine your latitude is on the equator and you are shooting a star directly west of your position, azimuth 270º. Since the earth turn 15' per minute of time, (15 nautical miles) the altitude of that star will get lower at the same rate, 15' per minute and 60' in four minutes. Attached are pages from H.O. 249 to illustrate this. Look at the first column on page 8 of the PDF file which is the 0º page of H.O. 249 volume 2 and you will see that the altitude decreases exactly one degree (60') for each one degree increase of LHA which takes four minutes of clock time. This also works with H.O. 249 volume 1, see page 11 and look at Procyon at LHA Aries of 45 to 48.
What happens at a different latitude? The earth still turns at the same rate but the minutes of longitude become smaller as you move away from the equator based on the cosine of the latitude. For example, at a latitude of 60º a degree of longitude is only half as long as it is at the equator since the cosine of 60º in .5 (30 nautical miles) and the change of altitude for a sight on an azimuth of 270º should also be one half or 30' per degree of LHA change. Look at the all columns on page 10 of the PDF file, which is the 60º page, at LHA 85º to 90º which results in a 90º (270º) azimuth and you will see that the altitude changes at the predicted rate, 30' per degree of LHA change. Also look at Capella for LHA 18 to 32 on page 13 to see that this also works for selected stars.
But what happens if the azimuth is not straight east or west? In this case the change of altitude is related to the cosine of the difference in the azimuth from east or west (which just happens to be the same as the sine of the azimuth) times the rate of change for the straight east and west cases. Using, for example, cases where the azimuth is 30º (sin is .5), which is 60º (cos is .5) from east, the change in altitude should be at half the rate of the east case since the cosine of 60º is .5. Look at page 8 for 0º latitude LHA 6 to 7 and declinations of 11 to 12 (producing azimuths of 30º) show changes of altitude at a rate of 30' per degree of LHA change, just as expected, one half the rate for the straight east case. Look at page 9 for the 60º latitude, LHA 25 to 28 and declination zero for 150º azimuth gives a rate of 15' per degree of LHA change (one half of one half of 60') and look at page 11, Capella LHA 115 to 117 and page 13, Betelgeuse LHA 64 to 65 for examples for selected stars.
These changes are the basis for the "Motion of the Body" (MOB) adjustment tables attached as pages 5 and 7. Review these tables and you will see they produce the same resulting changes in altitude as shown in the previous discussion. Another way to look at this is that you are interpolating for minutes of LHA (LHA not being whole degrees) as discussed in the previous thread regarding such interpolations using minutes of time rather than minutes of LHA as the entering arguments.
Now we come to, what might be confusing, the sign to apply to these adjustment. Consider the first example, on the equator looking straight west. Since the altitude is decreasing as time goes by, if the sight is taken before fix time (the time used for the computation) then the measured altitude, Hs, should be higher than that computed for the fix time by the amount shown in the "MOB" table or 15' higher for each minute the sight is earlier or one degree if the shot is four minutes before fix time. This adjustment would be added to the Hc for the fix time to compute the Hc for the earlier sight so the sign would be "+" so as to arrive at the same intercept. So for any body observed to the west the sign will be "+" and, by the same logic, the sign will be "-" for any body observed to the east. If a shot were taken after the fix time (which is not normally done) you would reverse the signs of these adjustments.
The MOB table and also the MOO tables have a confusing table specifying what sign to use. You would use the listed sign if the sight were earlier than the fix time and the adjustment was to be applied to the observed altitude. Since normal practice is to make the adjustment to Hc, not to Ho, you must reverse the listed signs. If the shot were taken after the fix time you would reverse the already reversed signs and used the listed signs (whew). But for normal flight navigation cases just remember to reverse the listed signs as you make the adjustments to Hc.
The next installment will discuss the "motion of the observer" adjustment.
gl
Gary J. LaPook wrote:
I was alaready thinking about doing that and will try to get it done in the next couple of days.
gl
jean-philippe planas wrote:
Gary,
I also enjoyed your very clear article.
However, could it be possible that you provide the list with a practical exercice (example) with figures taken from a real LOP computation involving 3 bodies shooting in the air to illustrate the process?
JPP
--- On Sun, 7/13/08, Frank Reed <FrankReedCT@aol.com> wrote:
From: Frank Reed <FrankReedCT@aol.com>
Subject: [NavList 5822] Re: Celestial up in the air
To: "NavList" <NavList@fer3.com>
Date: Sunday, July 13, 2008, 3:12 PM
Gary, I very much enjoyed your article and learned quite a bit from it. Well- written and clear! -FER
--~--~---------~--~----~------------~-------~--~----~
Navigation List archive: www.fer3.com/arc
To post, email NavList@fer3.com
To , email NavList-@fer3.com
-~----------~----~----~----~------~----~------~--~---