NavList:

I have been keenly following all the recent postings on measuring angles without a protractor and wondering if anyone would take the idea to the next logical step and use it in the vertical rather than the horizontal plane?

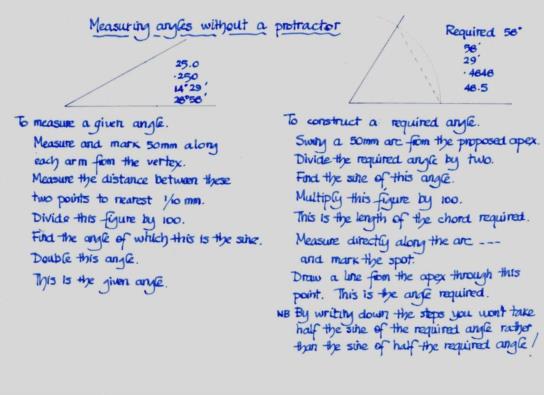
For some years I have been playing around with simple chord based quadrants and hence measuring angles without a protractor but it was only last year, when I unsuccessfully tried to make a quadrant out of a CD, that I discovered another simple way to measure any angle on paper. The method is based on the theorem that states that " the line drawn from the center of a circle at right angles to a chord bisects the chord". The formula for calculating the required angle is " A = 2 X ASN ( Chord / 2R ) " where R is a length of 50mm measured along each arm of the angle and the chord is the distance between these two points measured to the nearest tenth of a mm. This makes for some very simple maths . The method to measure and construct angles is shown in the first attachment.

An angle in the vertical plane can be measured as shown in the second attachment. Two random angles were drawn from the same point on a piece of card. A reference point was marked on the base line of the angles exactly 100mm from the vertex. A washer was tied to a length of cotton and the cotton attached to the card in such a way that when suspended from the vertex with blue tack the center of the washer lay exactly over the reference point when held vertically. The cotton and washer act as a plumb bob and remained vertical whilst the card was rotated until the center of the washer lay over the arm of the first angle. The card was gently laid on a horizontal surface and the spot marked at the exact center of the washer. This was then repeated for the second angle.

Now the two chords can be measured and the angles calculated using the above formula. Because a reference length of 100mm has been used an extra step is needed. The chord length must be divided by 2R (200). Divide by 100 and then by two. Keeping the radius in increments of 50mm makes for easy calculations. The angle can now be measured with a protractor.

The third attachment shows the next logical step. An octant made from a filing card with a sight made by carefully folding two flaps. When pointed directly at the sun the shadow of the horizontal flap is at its thinnest when projected onto the vertical flap. The card was just the right height to permit a radius length of 150mm. A line on the card provides the perfect reference line. The plumb bob was held by blue tack on the back of the card and the whole mounted on a stout notebook with masking tape. The photo was taken after the first use of this simple octant and I was quite astonished to achieve an intercept of less than 2nm. Needless to say this was impossible to repeat on later attempts but it does show the practical use of measuring angles without a protractor.

John Brown

Adelaide, South Australia.
----------------------------------------------------------------
NavList message boards and member settings: www.fer3.com/NavList
Members may optionally receive posts by email.
To cancel email delivery, send a message to NoMail[at]fer3.com
----------------------------------------------------------------