NavList:

   

Reply

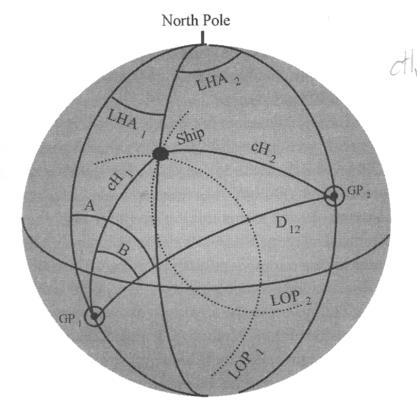
John Karl wrote, in [10556]

"George, and others who may be interested --

Remember we navigators are sensitive to terminology (negative longitudes,
assumed positions, dip, index mirrors, etc.).  So please don't call the two
fixes "ambiguous" in the 2-body problem.  The key point that everyone needs
to agree on is, that, given only the altitudes of two bodies and their
coordinates, there are TWO UNAMBIGUOUS fixes.  Other than outside
information, no computer code, no reformulation of the equations, can
distinguish between these two fixes.  Does anyone on the List disagree with
that??  If so, tell me where I'm going astray."

==================

Well, I agree with the last bit, that "Other than outside information, no
computer code, no reformulation of the equations, can distinguish between
these two fixes." And to me, that's an example of the very meaning of the
word "ambiguity"; that there are two possible answers, and the ship can only
be at one of them. Am I misunderstanding the meaning of that word? Is John?
His objection to it is as mysterious, to me, as his continued, and repeated,
objection to the word "assumed position" in St Hilaire's method. These
semantic questions seem a bit of a distraction from the reality, though I
concur with John that we should try to agree about the meaning of the words
we use.

Anyway, until I can find a better word, I will continue to use "ambiguous"
in that context of the two-body fix. And in solving that problem, two levels
of ambiguity arise. First, the one that John refers to above, that can only
be resolved by the navigator knowing roughly where the ship is. And a second
level of ambiguity, that arises in deducing a local hour angle from its
cosine, which is less serious in that it can be resolved by logical
procedures only, and needs no navigator's judgment, as I will show later.

==================

John wrote in [10496] ." It should be apparent both from Fig 7.3 and from
Eqs 7.5a-e, that these five equations do not contain information on the zero
of longitude.  Thus they can not determine longitude, which must be
determined from another source -- such as the navigator."

and again, in [10511], "...the fact that no set of equations derived from
Fig 7.3 can determine longitude because there is no longitude information in
the figure".

I don't follow that. Surely, those equations determine LHA1, although with
an ambiguity between two possible values. And GHA1 is known. Then longitude
is the difference between them, as shown in 7.5f. , Lon = LHA1 - GHA1.
Simple as that. Yes, we know there will be two solutions, the two
crossing-points of the circles, and choosing between those is where the
navigator's judgment comes in. But there's no extra ambiguity, on top of
that one, that calls for a navigator's judgment to resolve, if we go about
the problem in a careful way.

==================

Attached is fig 7.3, from John Karl's nice book, "Celestial Navigation in
the GPS age", page 79 in my 2007 edition. It shows position circles around
two stars, star1 above GP1, star2 above GP2. The ship must be at one of the
two intersections of those dotted circles. The radii of those circles are
marked cH1 and cH2, referring to the co-altitude, or Zenith distance, of
each star, though the resulting equations use the altitudes H1 and H2, where
H1 = 90 - cH1. The only thing I would question, in that diagram, is the way
LHA2 is marked. Hour angle of a body is always measured westerly from the
observer, but here it's shown going easterly. I doubt if that matters, much.
The declinations of the stars, d1 and d2, aren't shown as such on the
diagram.

I will follow John's notation, and use the same (Gauss) equations, but be a
bit more rigorous (in my view) in defining some angles.

The ship can be anywhere in the world, the star GPs can be anywhere visible
from the ship (i.e. within 90 degrees) and the stars can be freely labelled
1 and 2, without worrying about which star is east of the other, or of the
ship. There can be an advantage in labelling star1 to be the one with
azimuth furthest from the observer's North-South line, but it's not a
requirement.

7.5a and 7.5b deal with the spherical triangle GP1 - N Pole -GP2. 7.5a
determines cos D12, the great-circle distance D12 between GP1 and GP2.
angle. As this arc-length can only be in the range 0 to 180 degrees, no
ambiguity arises in taking arc-cos to get D12.
7.5a is
cos D12 = sin d1 sin d2 =cos d1 cos d2 cos (GHA1 -GHA2).

GHA1 and GHA2 are both measured Westerly from Greenwich, and we will need to
note the sign of their difference. An easy way to specify that test is to
see if sin (GHA1 - GHA2) is negative, in which case GP2 is west of GP1. The
numerical value of that sine isn't needed, just its sign.

In 7.5b, we're going to specify angle A more carefully, as the bearing from
GP1, measured clockwise from North, of the great circle passing through GP2.
Equation 7.5b is-
cos A = (sin d2 -sin d1 cos D12) / cos d1 sin D12
but next we introduce a step-
if sin (GP1-GP2) is negative, A = 360 - A.
A is now in the correct quadrant, with no ambiguity. It can be anywhere from
0 to 360 degrees.

Next we switch attention to spherical triangle GP1 - ship - GP2.
Angle B is determined from 7.5c
cos B = (sin H1 - cos D12 sin H1) / sin D12 cos H1.
Because it's taken from an arc-cos, B has two solutions, equal in value,
somewhere between 0 and 180 degrees, but opposite in sign. Because we will
use both solutions, we don't need to bother about defining a direction in
which angle B is positive.

Next, we need to look at spherical triangle GP1 - N Pole - ship.
In this, it will be convenient to refer to the angle C, not marked as such
on the diagram. This is the great-circle bearing of the ship from GP1,
measured clockwise from North, 0 to 360 degrees. Clearly, C has two possible
values, which we could label Ci and Cj, depending on the sign of B from
equation 7.5c.
Ci = A-B
Cj = A+B
 which correspond to the ship being at two crossing-points. Only one of
those is shown on the diagram, that for A-B. The other, for A+B, would be
the bearing from GP1 of the other intersection between the dotted circles.

From this triangle comes equation 7.5d,
sin lat = sin d1 sin H1 +cos d1 cos H1 cos(A-B),
which we can now write as
sin lat = sin d1 sin H1 +cos d1 cos H1, cos C

Now we have to take the two alternatives separately
Start with Ci = A-B, and with this goes-
sin lati= sin d1 sin H1 +cos d1 cos H1 cosCi
Ci can lie in the range -180 to +360.

The other alternative is-
Cj = A+B,
and with that goes
sin latj= sin d1 sin H1 +cos d1 cos H1 cosCj
in which C2 can have a value between 0 and 540 degrees.

Note that these values of Ci and Cj represent alternative true bearings of
ship from GP1.
Having found those two latitudes, lati and latj, now we need to find the
corresponding hour angles of GP1, LHA1i and LHA1j

From that same triangle GP1 - N Pole - ship, comes 7.5e
cos LHA1 = (sin H1 - sin d1 sin Lat) / cos d1 cos Lat
and we have to take the two alternatives, firstly-
cos LHA1i = (sin H1 - sin d1 sin Lat) / cos d1 cos Lati
annd now we come to the original stumbling-block, that these changes are an
attempt to overcome. Because when we try to obtain that value of LHA1i from
its cosine, we get two solutions; equal angles, positive and negative. It's
an additional layer of ambiguity. Which one is correct?

We choose according to the value of Ci, which is the true bearing of the
ship from GP1. We know that if that angle Ci (after adding or subtracting
360 degrees as necessary) is between  0 and 180 degrees, then the ship is
somewhere eastward of GP1, in which case LHA1i must be positive. And vice
versa, of course, if between 180 and 360. An easy way to state that choice
is by the sign of sin Ci.

So, having arrived at a solution for LHA1i above, we can introduce a new
line-
if Sin Ci is negative, LHA1i = 360 - LHA1i, to remove that second-layer of
ambiguity.
And then, derive the longitude (Eastitude, as John Karl prefers)  from 7.5f,
as before, from
Loni = LHA1i - GHA1
That provides one of the two possible positions, (Lati, Loni).

We have already determined the other latitude Latj, from the value of Cj.
Next we find LHA1j from 7.5e, as-
cos LHA1j = (sin H1 - sin d1 sin Lat) / cos d1 cos Latj
and if Sin Cj is negative, LHA1j = 360 - LHA1j

and from that Lonj = LHA1ij- GHA1
and the job is done.
================

Now, I don't wish to pretend that what's written above is at all elegant.
But it's a logical procedure that relies on navigator's judgment, only in
deciding between those two crossings of the position circles; nowhere else.

I have dealt with every step, in excruciating detail, to try to get it
right, but really, it adds very little complexity to the procedure outlined
by John. I'm not claiming that his procedure is mathematically wrong. But,
unless great care is taken in getting the quadrants right, as I have tried
to do, it will give the unwary navigator wrong answers.

George.

contact George Huxtable, at  george@hux.me.uk
or at +44 1865 820222 (from UK, 01865 820222)
or at 1 Sandy Lane, Southmoor, Abingdon, Oxon OX13 5HX, UK.

--~--~---------~--~----~------------~-------~--~----~
NavList message boards: www.fer3.com/arc
Or post by email to: NavList@fer3.com
To , email NavList+@fer3.com
-~----------~----~----~----~------~----~------~--~---

File:

   

Reply